
 如图,点E,F在BC上,BE=CF,∠AFE=∠DEF,∠B=∠C,求证:AB=DC.
如图,点E,F在BC上,BE=CF,∠AFE=∠DEF,∠B=∠C,求证:AB=DC.  三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3或5 | D. | 3或4或5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
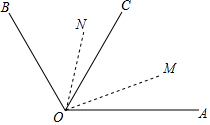 如图,在∠AOB的内部作射线OC,使∠AOC与∠AOB互补,将射线OA,OC同时绕点O分别以每秒12°,每秒8°的速度按逆时针方向旋转,旋转后的射线OA,OC分别记为OM,ON,设旋转时间为t秒.已知t<30,∠AOB=114°.
如图,在∠AOB的内部作射线OC,使∠AOC与∠AOB互补,将射线OA,OC同时绕点O分别以每秒12°,每秒8°的速度按逆时针方向旋转,旋转后的射线OA,OC分别记为OM,ON,设旋转时间为t秒.已知t<30,∠AOB=114°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com