练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

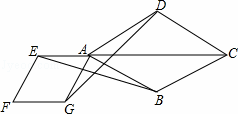
    如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，连接EB，GD．

    （1）求证：EB=GD；

    （2）若∠DAB=60°，AB=2，AG=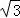，求GD的长．


                  （1）证明：∵菱形AEFG∽菱形ABCD，

    ∴∠EAG=∠BAD，

    ∴∠EAG+∠GAB=∠BAD+∠GAB，

    ∴∠EAB=∠GAD，

    ∵AE=AG，AB=AD，

    ∴△AEB≌△AGD，

    ∴EB=GD；

    （2）解：连接BD交AC于点P，则BP⊥AC，

    ∵∠DAB=60°，

    ∴∠PAB=30°，

    ∴BP=AB=1，

    AP==，AE=AG=，

    ∴EP=2，

    ∴EB===，

    ∴GD=．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    从广州到某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400千米，普通列车的行驶路程是高铁的行驶路程的1.3倍．

    （1）求普通列车的行驶路程；

    （2）若高铁的平均速度（千米/时）是普通列车平均速度（千米/时）的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若等腰三角形的两条边长分别为7cm和14cm，则它的周长为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，则满足条件的点P的个数是（　　）

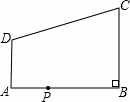
    A．  1个           B．2个           C．3个           D． 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知在Rt△OAC中，O为坐标原点，直角顶点C在x轴的正半轴上，反比例函数y=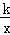（k≠0）在第一象限的图象经过OA的中点B，交AC于点D，连接OD．若△OCD∽△ACO，则直线OA的解析式为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


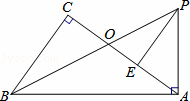
    如图，在Rt△ABC中，∠C=90°，Rt△BAP中，∠BAP=90°，已知∠CBO=∠ABP，BP交AC于点O，E为AC上一点，且AE=OC．

    （1）求证：AP=AO；

    （2）求证：PE⊥AO；

    （3）当AE=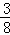AC，AB=10时，求线段BO的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果两个相似三角形的面积比是1：2，那么它们的周长比是（　　）

    A．  1：2          B．1：4          C．1：        D． 2：1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图．在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CF交AD于点F，点E是AB的中点，连接EF．

    （1）求证：EF∥BC；

    （2）若四边形BDFE的面积为6，求△ABD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


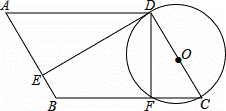
    已知：如图，四边形ABCD为平行四边形，以CD为直径作⊙O，⊙O与边BC相交于点F，⊙O的切线DE与边AB相交于点E，且AE=3EB．

    （1）求证：△ADE∽△CDF；

    （2）当CF：FB=1：2时，求⊙O与▱ABCD的面积之比．

    查看答案和解析>>

    同步练习册答案