
【题目】用一条长为18的绳子围成一个等腰三角形.
(1)若等腰三角形有一条边长为4,它的其它两边是多少?
(2)若等腰三角形的三边长都为整数,请直接写出所有能围成的等腰三角形的腰长.
【答案】(1)其他两边分别为4和7;(2)y=2时,x=8,y=4时,x=7,y=8时,x=5.
【解析】
(1)根据等腰三角形的性质即可求出答案.
(2)设等腰三角形的三边长为x、x、y,根据题意可知y<9,y是2的倍数,从而可求出答案.
解:(1)当等腰三角形的腰长为4,
∴底边长为18﹣4×2=10,
∵4+4<10,
∴4、4、10不能组成三角形,
当等腰三角形的底边长为4,
∴腰长为(18﹣4)÷2=7,
∵4+7>7,
∴4、7、7能组成三角形,
综上所述,其他两边分别为4和7.
(2)设等腰三角形的三边长为x、x、y,
由题意可知:2x+y=18,
且2x>y,
∴y<9,
∵x=![]() =9﹣
=9﹣![]() ,x与y都是整数,
,x与y都是整数,
∴y是2的倍数,
∴y=2时,x=8,
y=4时,x=7,
y=8,x=5.


科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.
(1)求FG的长;
(2)直接写出图中与△BHG相似的所有三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=CD,E,F,G,H分别为AB,BC,CD,AD的中点,顺次连接E,G,F,H,求证:四边形EFGH是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )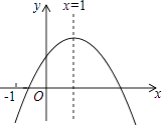
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+6分别交x轴、y轴于A、B两点,抛物线y=﹣
x+6分别交x轴、y轴于A、B两点,抛物线y=﹣ ![]() x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.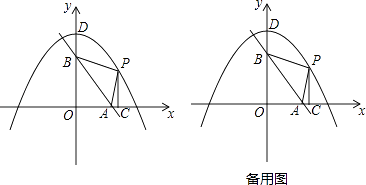
(1)点A的坐标为 , 点D的坐标为;
(2)探究发现:
①假设P与点D重合,则PB+PC=;(直接填写答案)
②试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由;
(3)试判断△PAB的面积是否存在最大值?若存在,求出最大值,并求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
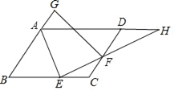
【题目】如图所示,在ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD于F.
(1)求证:CE=CF;
(2)延长AD、EF交于点H,延长BA到G,使AG=CF,若AD=7,DF=3,EH=2AE,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_______cm/s时,能够使△BPE≌△CQP.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com