
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正确结论个数是( )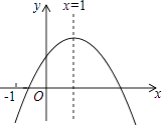
A.1
B.2
C.3
D.4
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,则
,则![]() ______.
______.

【答案】-1
【解析】
将点A的坐标代入两直线解析式得出关于m和b的方程组,解之可得.
解:由题意知![]() ,
,
解得![]() ,
,
故答案为:![]() .
.
【点睛】
本题主要考查两直线相交或平行问题,解题的关键是掌握两直线的交点坐标必定同时满足两个直线解析式.
【题型】填空题
【结束】
11
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则△AFC的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距4千米.上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题
两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” B.345和513互为“调和数
C.2018和8120互为“调和数” D.两位数![]() 和
和![]() 互为“调和数”
互为“调和数”
(2)若A、B是两个不等的两位数,A=![]() ,B=
,B=![]() ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18的绳子围成一个等腰三角形.
(1)若等腰三角形有一条边长为4,它的其它两边是多少?
(2)若等腰三角形的三边长都为整数,请直接写出所有能围成的等腰三角形的腰长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中A(0,a),B(b,0),且a、b满足![]() 作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.
作射线BA,AB=10,动点P从B开始沿射线BA以每秒2个单位长度的速度运动,运动时间为t.

(1)求点A、B的坐标;
(2)设△AOP的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)点M为线段OP的中点,连接AM,当点P在线段BA上时,△AOM的面积为△AOB面积的![]() 时,求出t值,并求出点M到x轴距离.
时,求出t值,并求出点M到x轴距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.
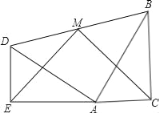
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则DF的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com