
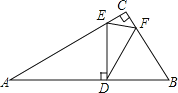
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
【答案】![]() 或
或![]()
【解析】
试题由于∠EDF=30°,且DE总垂直于AB,因此∠FDB=60°,此时发现△FDB是等边三角形,那么BD=BF,2﹣AD=1﹣CF,即AD=CF+1.由于∠C是直角,当△CEF与△DEF相似时,△DEF必为直角三角形,那么可分两种情况讨论:①∠DEF=90°,此时,△CEF∽△DEF;②∠DFE=90°,此时△CEF∽△FED;可根据各相似三角形得到的比例线段求出CF的值,进而可求得AD的值.
解:∵∠EDF=30°,ED⊥AB于D,
∴∠FDB=∠B=60°,
∴△BDF是等边三角形;
∵BC=1,∴AB=2;
∵BD=BF,
∴2﹣AD=1﹣CF;
∴AD=CF+1.
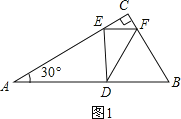
①如图1,∠FED=90°,△CEF∽△EDF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CF=![]() ;
;
∴AD=![]() +1=
+1=![]() ;
;
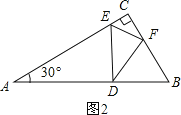
②如图2,∠EFD=90°,△CEF∽△FED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ;
;
解得,CF=![]() ;
;
∴AD=![]() +1=
+1=![]() .
.
故答案为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
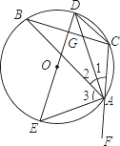
【题目】如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同。
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率。(请利用树状图或列表法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是( )
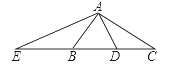
A. △AED与△ACB B. △AEB与△ACD C. △BAE与△ACE D. △AEC与△DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
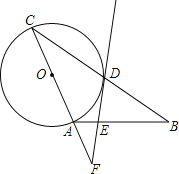
【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,![]() =
=![]() 时,求DE的长.
时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
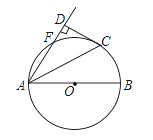
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程kx2﹣(4k+1)x+3k+3=0(k是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点.已知反比例函数y=![]() (m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
(m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com