
分析 根据轴对称的性质,首先准确找到点P的位置.根据菱形的性质,作点E′和E关于BD对称.则连接AE′交BD于点P,P即为所求作的点.PE+PA的最小值即为AE′的长.
解答 解:作点E′和E关于BD对称.则连接AE′交BD于点P,
∵四边形ABCD是菱形,AB=4,E为AD中点,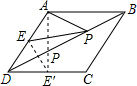
∴点E′是CD的中点,
∴DE′=$\frac{1}{2}$DC=$\frac{1}{2}$×4=2,AE′⊥DC,
∴AE′=$\sqrt{A{D}^{2}-DE{′}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.


科目:初中数学 来源: 题型:解答题
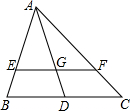 如图,△ABC中,EF∥BC,AD交EF于G.
如图,△ABC中,EF∥BC,AD交EF于G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2015 | B. | 1036 | C. | 518 | D. | 259 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )| A. | -a<-b<a<b | B. | a<-b<b<-a | C. | -b<a<-a<b | D. | a<b<-b<-a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
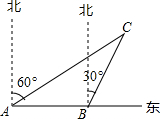 如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?
如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com