
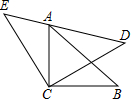
 如图,△ACB和△ECD都是等腰直角三角形,CA=CA,CE=CD,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)
如图,△ACB和△ECD都是等腰直角三角形,CA=CA,CE=CD,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD) 分析 连结BD,根据等腰直角三角形的性质就可以得出△AEC≌△BDC,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出结论.
解答 证明:连接BD,如图所示: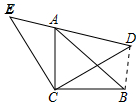
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-∠ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD
在△AEC和△BDC中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACE=∠BCD}&{\;}\\{EC=DC}&{\;}\end{array}\right.$,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.
点评 本题考查了等腰直角三角形的性质的运用,直角三角形的判定及性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
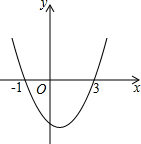 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
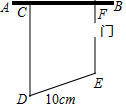 张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD∥EF),如图所示,若DE的长为10m,则梯形场地CDEF的最大面积是多少?
张大伯利用一堵旧墙AB,用长50m的篱笆围成一个留有1m宽的门的梯形场地CDEF(CD∥EF),如图所示,若DE的长为10m,则梯形场地CDEF的最大面积是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com