
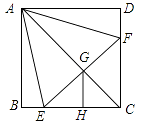
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若 ![]() ,则
,则 ![]() =( )
=( )
A.6
B.4
C.3
D.2
【答案】A
【解析】∵四边形ABCD是正方形,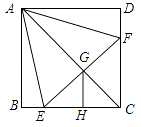
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
∵AE=AF,AB=AD,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∴△CEF是等腰直角三角形,
∵AE=AF,
∴AC垂直平分EF,
∴EG=GF,
∵GH⊥CE,
∴GH∥CF,
∴△EGH∽△EFC,
∵S△EGH=3,
∴S△EFC=12,
∴CF= ![]() ,EF=
,EF= ![]() ,
,
∴AF= ![]() ,设AD=x,则DF=x﹣
,设AD=x,则DF=x﹣ ![]() ,
,
∵AF2=AD2+DF2 ,
∴( ![]() )2=x2+(x﹣
)2=x2+(x﹣ ![]() )2 ,
)2 ,
∴x= ![]() ,
,
∴AD= ![]() ,DF=
,DF= ![]() ,
,
∴S△ADF= ![]() ADDF=6.
ADDF=6.
故答案为:A.
根据正方形的性质及等边三角形的性质易证明AE=AF,AB=AD,根据直角三角形全等判定证明Rt△ABE≌Rt△ADF,得出BE=DF,从而证得CE=CF,得出△CEF是等腰直角三角形,再证明GH∥CF,得出△EGH∽△EFC,根据相似三角形的性质及S△EGH=3,求出△EFC的面积,从而求出AF和CE的长,然后设AD=x,利用勾股定理求出AD的长及DF的长,根据三角形的面积公式即可得出答案。


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )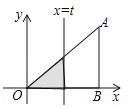
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
小明同学遇到下列问题:
解方程组 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y,
这时原方程组化为 ,解得
,解得![]() ,
,
把![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得![]() 解得
解得![]() .
.
所以,原方程组的解为![]()
(解决问题)
请你参考小明同学的做法,解决下面的问题:
(1)解方程组 ;
;
(2)已知方程组![]() 的解是
的解是![]() ,求方程组
,求方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
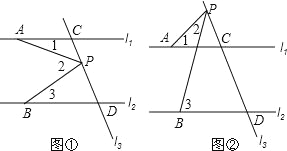
【题目】已知直线 l1∥l2,l3 和 l1,l2 分别交于 C,D 两点,点 A,B 分别在线 l1,l2 上,且位于 l3 的左 侧,点 P 在直线 l3 上,且不和点 C,D 重合.
(1)如图 1,有一动点 P 在线段 CD 之间运动时,试确定∠1、∠2、∠3 之间的关系,并给出证明;
(2)如图 2,当动点 P 在线段 CD 之外运动时,上述的结论是否成立?若不成立,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的一点,
边上的一点,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着边
出发,以每秒1个单位的速度沿着边![]() 向终点
向终点![]() 运动,连接
运动,连接![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.

(1)求![]() 的长;
的长;
(2)当![]() 为多少秒时,
为多少秒时,![]() 是直角三角形?
是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
A.7
B.11
C.13
D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com