练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形中，，，为边上的一点，，动点从点出发，以每秒1个单位的速度沿着边向终点运动，连接．设点运动的时间为秒．

    （1）求的长；

    （2）当为多少秒时，是直角三角形？

    【答案】（1）5；（2）当t=7或秒时，△BPE为直角三角形．

    【解析】

    （1）根据勾股定理计算即可；

    （2）分∠BPE＝90°、∠BEP＝90°两种情况，根据勾股定理计算．

    解：（1）由题意知，CD=AB=10，DE=7，BC=4

    CE=CD-DE=10﹣7=3，

    在Rt△CBE中，BE=；

    （2）①当以P为直角顶点时，即∠BPE=90°，

    AP=10﹣3=7，则t=7÷1=7（秒），

    ②当以E为直角顶点时，即∠BEP=90°，由勾股定理得

    BE2+PE2=BP2，

    设AP=t，

    ，

    即52+42+（7﹣t）2=（10﹣t）2，

    解得，t=，

    当t=7或秒时，△BPE为直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了贯彻落实中央提出的“厉行节约，反对浪费”的精神，某校学生自发组织了“保护水源，从我做起”的活动，学生们对我国“水资源问题”进行了调查，发现我国水资源越来越匮乏，可是人们的节约意识并不强.据查，仅某饮料厂每天从地下抽水达3500立方米左右.同学们采取问卷调查的方式，随机调查了本校150名同学家庭人均月用水量和节水措施情况.以下是根据调查结果作出的部分统计图：

    请根据以上信息，解答以下问题：

    （1）补全图①和图②；

    （2）为提高人们的节水意识，请你写出一条与图②中已明确的节水措施不同的节水措施.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D，下列四个结论：

    ①EF=BE+CF；

    ②∠BOC=90°+∠A；

    ③点O到△ABC各边的距离相等；

    ④设OD=m，AE+AF=n，则．

    其中正确的结论是____．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

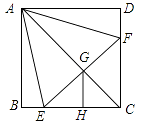
    【题目】如图，正方形ABCD中．点E，F分别在BC，CD上，△AEF是等边三角形．连接AC交EF于点G．过点G作GH⊥CE于点H．若 ，则 =（ ）

    A.6
    B.4
    C.3
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，AE⊥BC，CF⊥AD，垂足分别为E，F，AE，CF分别与BD交于点G和H，且AB= ．

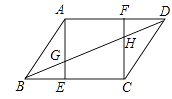
    （1）若tan∠ABE =2，求CF的长；
    （2）求证：BG=DH．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB=BC=10，以AB为直径作⊙O分别交AC，BC于点D，E，连接DE和DB，过点E作EF⊥AB，垂足为F，交BD于点P．

    （1）求证：AD=DE；
    （2）若CE=2，求线段CD的长；
    （3）在（2）的条件下，求△DPE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某年级共有300名学生．为了解该年级学生A，B两门课程的学习情况，从中随机抽取60名学生进行测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析．下面给出了部分信息．

    ．A课程成绩的频数分布直方图如下（数据分成6组：，，，，，）；

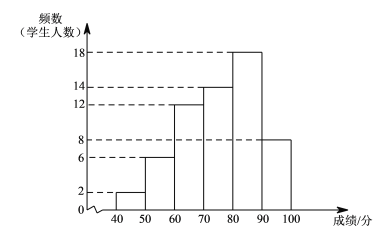
    ．A课程成绩在这一组是：

    70 71 71 71 76 76 77 78 79 79 79

    ．A，B两门课程成绩的平均数、中位数、众数如下：

    课程

    平均数

    中位数

    众数

    A

    B

    70

    83

    根据以上信息，回答下列问题：

    （1）写出表中的值；

    （2）在此次测试中，某学生的A课程成绩为76分，B课程成绩为71分，这名学生成绩排名更靠前的课程是________（填“A”或“B”），理由是_______；

    （3）假设该年级学生都参加此次测试，估计A课程成绩超过分的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解题： 学习了二次根式后，你会发现一些含有根号的式子可以写成另一个式子的平方，如3+2 =（1+ ）2 ， 我们来进行以下的探索：
    设a+b =（m+n ）2（其中a，b，m，n都是正整数），则有a+b =m2+2n2+2mn ，∴a=m+2n2 ， b=2mn
    ， 这样就得出了把类似a+b 的式子化为平方式的方法．
    请仿照上述方法探索并解决下列问题：
    （1）当a，b，m，n都为正整数时，若a﹣b =（m﹣n ）2 ， 用含m，n的式子分别表示a，b，得a= ， b=；
    （2）利用上述方法，找一组正整数a，b，m，n填空：﹣ =（﹣ ）2
    （3）a﹣4 =（m﹣n ）2且a，m，n都为正整数，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示在平面直角坐标系中，有长方形OABC，O是坐标原点，A(a,0）,C（0，b），且a,b满足

    （1）求A,B,C三点坐标；

    （2）如图2所示，长方形对角线OB、AC交于D点，若有一点P从A点出发，以1单位/秒速度向x轴负方向匀速运动，同时另一点Q从O出发，以2个单位/秒，沿长方形边长O-C-B顺时针匀速运动，当Q到达B点时P、Q同时停止运动，设P点开始运动时间为t，请问：当t为何值时有S△OCP≤S△ODQ ？

    查看答案和解析>>

    同步练习册答案