
【题目】如图1所示在平面直角坐标系中,有长方形OABC,O是坐标原点,A(a,0),C(0,b),且a,b满足![]()
(1)求A,B,C三点坐标;
(2)如图2所示,长方形对角线OB、AC交于D点,若有一点P从A点出发,以1单位/秒速度向x轴负方向匀速运动,同时另一点Q从O出发,以2个单位/秒,沿长方形边长O-C-B顺时针匀速运动,当Q到达B点时P、Q同时停止运动,设P点开始运动时间为t,请问:当t为何值时有S△OCP≤S△ODQ ?

【答案】(1)A(4,0)B(4,8)C(0,8);(2)![]() ≤t<4或4<t≤5.
≤t<4或4<t≤5.
【解析】
(1)由算术平方根的被开方数为非负数可求得a的值,继而求得b的值,再根据长方形的性质即可求得答案;
(2)分0≤t<4,t=4,4<t≤6三种情况分别讨论即可求得答案.
(1)由![]() ,得
,得
![]() ,
,
解得a=4,
所以b-2=6,
解得b=8,
所以A(4,0),C(0,8),
所以OA=4,OC=8,
又因为ABCD是长方形,
所以AB=OC=8,BC=OA=4,
所以C(4,8);
(2)过D作DE⊥OC于点E,则有DE=2,OE=CE=4,
①当0≤t<4时,如图(1),
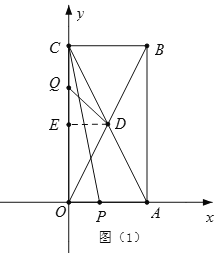
S△OCP=![]() OC·OP=
OC·OP=![]() ×8×(4-t),
×8×(4-t),
S△ODQ=![]() OQ·DE=
OQ·DE=![]() ×2t×2,
×2t×2,
令S△OCP≤S△ODQ,
即有![]() ×8×(4-t)≤
×8×(4-t)≤![]() ×2t×2,
×2t×2,
解得t≥![]() ;
;
②当t=4时,△OPC不存在,舍去;
③当4<t≤6时,如图(2)
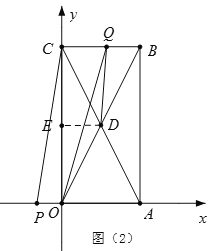
S△OCP=![]() OC·OP=
OC·OP=![]() ×8×(t-4),
×8×(t-4),
S△ODQ=S△OBC-S△OCQ-S△DBQ=![]() OC·BC-
OC·BC-![]() OC·CQ-
OC·CQ-![]() BQ·CE
BQ·CE
=![]() ×4×8-
×4×8-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×(8+4-2t)×4,
×(8+4-2t)×4,
令S△OCP≤S△ODQ,
即有![]() ×8×(t-4)≤
×8×(t-4)≤![]() ×4×8-
×4×8-![]() ×8×(2t-8)-
×8×(2t-8)-![]() ×(8+4-2t)×4,
×(8+4-2t)×4,
解得 t≤5,
综上所述,当![]() ≤t<4或4<t≤5时成立.
≤t<4或4<t≤5时成立.


科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的一点,
边上的一点,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿着边
出发,以每秒1个单位的速度沿着边![]() 向终点
向终点![]() 运动,连接
运动,连接![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.

(1)求![]() 的长;
的长;
(2)当![]() 为多少秒时,
为多少秒时,![]() 是直角三角形?
是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
A.7
B.11
C.13
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1个单位长度,其行走的路线如图所示,第1次移动到A1,第2次移动到A2……,第n次移动到An,则三角形OA2A2018的面积是( )
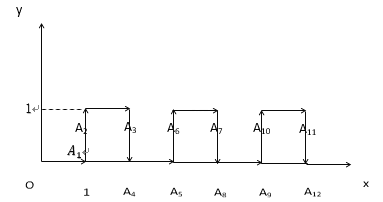
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在函数y1=﹣ ![]() (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com