
【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE. 求证:四边形BCDE是矩形.
【答案】证明:∵∠BAD=∠CAE, ∴∠BAD﹣∠BAC=∠CAE﹣∠BAC,
∴∠BAE=∠CAD,
∵在△BAE和△CAD中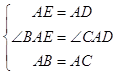
∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=CB,
∴四边形BCDE是平行四边形,
∵AE=AD,
∴∠AED=∠ADE,
∵∠BEA=∠CDA,
∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.
【解析】求出∠BAE=∠CAD,证△BAE≌△CAD,推出∠BEA=∠CDA,BE=CD,得出平行四边形BCDE,根据平行线性质得出∠BED+∠CDE=180°,求出∠BED,根据矩形的判定求出即可.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:

①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则![]() .
.
其中正确的结论是____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC∥AD,添加下列条件,不能判定四边形ABCD是平行四边形的是( )

A.AB=CDB.AB∥CDC.∠A=∠CD.BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
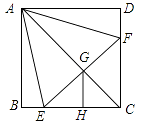
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若 ![]() ,则
,则 ![]() =( )
=( )
A.6
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.
(1)求证:AD=DE;
(2)若CE=2,求线段CD的长;
(3)在(2)的条件下,求△DPE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4 ![]() ,DE⊥AB于E.
,DE⊥AB于E.
(1)求DE的长.
(2)求证:AC=2OE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com