Question

【题目】在平面直角坐标系中，点O为坐标原点，直线y=﹣x+3与x轴、y轴相交于B、C两点，抛物线y=ax2+bx+3经过点B，对称轴为直线x=1．

（1）求a和b的值；

（2）点P是直线BC上方抛物线上任意一点，设点P的横坐标为t，△PBC的面积为S，求S与t之间的函数关系式，并写出t的取值范围；

（3）P为抛物线上的一点，连接AC，当∠BCP=∠ACO时，求点P的坐标．

Answer 1

【答案】(1) a=﹣1，b=2；(2) S△PBC =﹣t2+t（0＜t＜3）；(4)P点坐标为（4，﹣5）或（，）．

【解析】

试题分析：（1）由直线解析式可求得B、C两点坐标，结合对称轴，可求得a、b；（2）过点P作PE∥y轴交BC于点D，交x轴于点E，作CF⊥PD于点F，可用t表示出PD的长，则可示得S与t的关系式；（3）当点P在x轴下方时，过点A作AH⊥CP1，利用面积相等可求得AK、CK的比，再利用勾股定理可求得K点的坐标，则可求得直线CK解析式，结合P1在抛物线上可求得其坐标；当点P在x轴上方时，过点B作BM∥y轴，交CP2延长线于点M，可证明△CBK≌△CBM，则可求得M点坐标，可求得直线CM解析式，同理可求得P2点的坐标，则可求得P点坐标．

试题解析：（1）∵直线y=﹣x+3与x轴、y轴相交于B、C两点，

∴B（3，0），C（0，3），

∴9a+3b+3=0，

∵抛物线对称轴为直线x=1，

∴=1，

∴a=﹣1，b=2；

（2）如图1，过点P作PE∥y轴交BC于点D，交x轴于点E，作CF⊥PD于点F，

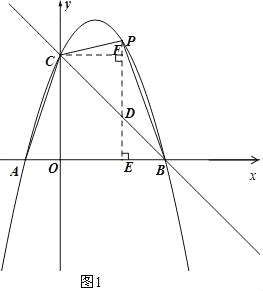
∵P（t，﹣t2+2t+3），

∴D（t，﹣t+3），

∵点P是直线BC上方，

∴PD=﹣t2+2t+3﹣（﹣t+3）=﹣t2+3t，

∴S△PBC=S△PCD+S△PBD=PDCF+PDBE=PDOB=×3（﹣t2+3t）=﹣t2+t（0＜t＜3）；

（3）①如图2，当∠BCP1=∠ACO时，过点A作AH⊥CP1，

∵OA=1，OC=3，

∴AC= ，

∵∠BCP1=∠ACO，

∴∠ACH=45°，

∴AH= ，

∵S△ACK=AKOC=CKAH，

∴ ，

设K=π，CK=3m，OK=m﹣1，

在Rt△COK中，OC2+OK2=CK2

∴32+（m﹣1）2=（3m）2，解得m= ，

∴K（ ，0），

∴直线CK解析式为y=﹣2x+3，

∴P1（n，﹣2n+3）

∵P1在抛物线y=﹣x2+2x+3上，

∴P1（4，﹣5）；

②如图2，∠BCP2=∠ACO时，过点B作BM∥y轴，交CP2延长线于点M，

在△CBK和△CBM中

∴△CBK≌△CBM（ASA），

∴BK=BM=，

∴M（3，），

∴直线CM的解析式为y=﹣x+3，

∴P2（m，﹣m+3）

∵P2在抛物线上，

∴P2（，），

∴P点坐标为（4，﹣5）或（，）．