
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+cгыxжсНЛгкЕуAЃЈЉ2ЃЌ0ЃЉЃЌЕуBЃЈ4ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ8ЃЉЃЌСЌНгBCЃЌгжвбжЊЮЛгкyжсгвВрЧвДЙжБгкxжсЕФЖЏжБЯпlЃЌбиxжсе§ЗНЯђДгOдЫЖЏЕНBЃЈВЛКЌOЕуКЭBЕуЃЉЃЌЧвЗжБ№НЛХзЮяЯпЁЂЯпЖЮBCвдМАxжсгкЕуPЃЌDЃЌEЃЎ
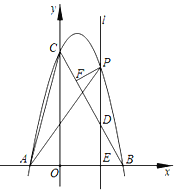
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНгACЃЌAPЃЌЕБжБЯпlдЫЖЏЪБЃЌЧѓЪЙЕУЁїPEAКЭЁїAOCЯрЫЦЕФЕуPЕФзјБъЃЛ
ЃЈ3ЃЉзїPFЁЭBCЃЌДЙзуЮЊFЃЌЕБжБЯпlдЫЖЏЪБЃЌЧѓRtЁїPFDУцЛ§ЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ yЃНЉx2+2x+8ЃЛЃЈ2ЃЉЕуPЃЈ![]() ЃЉЃЛЃЈ3ЃЉ
ЃЉЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЁЂBЁЂCЕФзјБъДњШыЖўДЮКЏЪ§БэДяЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉжЛгаЕБЁЯPEAЃНЁЯAOCЪБЃЌPEAЁїЁзAOCЃЌПЩЕУЃКPEЃН4AEЃЌЩшЕуPзјБъЃЈ4kЉ2ЃЌkЃЉЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉРћгУRtЁїPFDЁзRtЁїBOCЕУЃК ![]() ЃЌдйЧѓГіPDЕФзюДѓжЕЃЌМДПЩЧѓНтЃЎ
ЃЌдйЧѓГіPDЕФзюДѓжЕЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉНЋЕуAЁЂBЁЂCЕФзјБъДњШыЖўДЮКЏЪ§БэДяЪНЕУЃК ЃЌ
ЃЌ
НтЕУЃКa= -1ЃЌb=2ЃЌc=8ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉx2+2x+8ЃЛ
ЃЈ2ЃЉЁпЕуAЃЈЉ2ЃЌ0ЃЉЁЂCЃЈ0ЃЌ8ЃЉЃЌ
ЁрOAЃН2ЃЌOCЃН8ЃЌ
ЁпlЁЭxжсЃЌЁрЁЯPEAЃНЁЯAOCЃН90ЁуЃЌ
ЁпЁЯPAEЁйЁЯCAOЃЌ
ЁржЛгаЕБЁЯPEAЃНЁЯAOCЪБЃЌPEAЁїЁзAOCЃЌ
ДЫЪБ![]() ЃЌМДЃК
ЃЌМДЃК![]() ЃЌ
ЃЌ
ЁрAEЃН4PEЃЌ
ЩшЕуPЕФзнзјБъЮЊkЃЌдђPEЃНkЃЌAEЃН4kЃЌ
ЁрOEЃН4kЉ2ЃЌ
НЋЕуPзјБъЃЈ4kЉ2ЃЌkЃЉДњШыЖўДЮКЏЪ§БэДяЪНВЂНтЕУЃК
kЃН0Лђ![]() ЃЈЩсШЅ0ЃЉЃЌдђЕуPЃЈ
ЃЈЩсШЅ0ЃЉЃЌдђЕуPЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉдкRtЁїPFDжаЃЌЁЯPFDЃНЁЯCOBЃН90ЁуЃЌ
ЁпlЁЮyжсЃЌ
ЁрЁЯPDFЃНЁЯCOBЃЌ
Ёр![]() ЁїPFDЁз
ЁїPFDЁз![]() ЁїBOCЃЌ
ЁїBOCЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрSЁїPDFЃН![]() SЁїBOCЃЌ
SЁїBOCЃЌ
ЖјSЁїBOCЃН![]() OBOCЃН
OBOCЃН![]() ЁС4ЁС8=16ЃЌ
ЁС4ЁС8=16ЃЌ
BCЃН![]() ЃЌ
ЃЌ
ЁрSЁїPDFЃН![]() SЁїBOCЃН
SЁїBOCЃН![]() PD2ЃЌ
PD2ЃЌ
МДЕБPDШЁЕУзюДѓжЕЪБЃЌSЁїPDFзюДѓЃЌ
НЋBЁЂCзјБъДњШывЛДЮКЏЪ§БэДяЪН![]() ЕУЃК
ЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФБэДяЪНЮЊЃКyЃНЉ2x+8ЃЌ
ЩшЕуPЃЈmЃЌЉm2+2m+8ЃЉЃЌдђЕуDЃЈmЃЌЉ2m+8ЃЉЃЌ
дђPDЃНЉm2+2m+8+2mЉ8ЃНЉЃЈmЉ2ЃЉ2+4ЃЌ
ЕБmЃН2ЪБЃЌPDЕФзюДѓжЕЮЊ4ЃЌ
ЙЪЕБPDЃН4ЪБЃЌЁрSЁїPDFЃН![]() PD2ЃН
PD2ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() гы
гы![]() жсКЭ
жсКЭ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() ХзЮяЯп
ХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() гыжБЯп
гыжБЯп![]() ЕФСэвЛИіНЛЕуЮЊ
ЕФСэвЛИіНЛЕуЮЊ![]() ЃЎ
ЃЎ
![]() Чѓ
Чѓ![]() ЕФжЕКЭХзЮяЯпЕФНтЮіЪН
ЕФжЕКЭХзЮяЯпЕФНтЮіЪН
![]() Еу
Еу![]() дкХзЮяЯпЩЯЃЌ
дкХзЮяЯпЩЯЃЌ![]() жсНЛжБЯп
жсНЛжБЯп![]() гкЕу
гкЕу![]() Еу
Еу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧвЫФБпаЮ
ЩЯЃЌЧвЫФБпаЮ![]() ЮЊОиаЮЃЎЩшЕу
ЮЊОиаЮЃЎЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ОиаЮ
ОиаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() Чѓ
Чѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНвдМА
ЕФКЏЪ§ЙиЯЕЪНвдМА![]() ЕФзюДѓжЕ
ЕФзюДѓжЕ
![]() НЋ
НЋ![]() ШЦЦНУцФкФГЕу
ШЦЦНУцФкФГЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЈЕу
ЃЈЕу![]() ЗжБ№гы
ЗжБ№гы![]() ЕуЖдгІ)ЃЌШє
ЕуЖдгІ)ЃЌШє![]() ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌЧыжБНгаДГіЕу
ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЫдкдЫЖЏЪБЕФаФЬјЫйТЪЭЈГЃКЭШЫЕФФъСфгаЙиЃЎШчЙћгУ![]() БэЪОвЛИіШЫЕФФъСфЃЌгУ
БэЪОвЛИіШЫЕФФъСфЃЌгУ![]() БэЪОе§ГЃЧщПіЯТетИіШЫдкдЫЖЏЪБЫљФмГаЪмЕФУПЗжаФЬјЕФзюИпДЮЪ§ЃЌФЧУД
БэЪОе§ГЃЧщПіЯТетИіШЫдкдЫЖЏЪБЫљФмГаЪмЕФУПЗжаФЬјЕФзюИпДЮЪ§ЃЌФЧУД![]() ЃЎ
ЃЎ
ЃЈ1ЃЉвЛИі45ЫъЕФШЫдЫЖЏЪБ10УыаФЬјЕФДЮЪ§ЮЊ22ДЮЃЌЫћ__________ЃЈЬюЁАгаЁБЛђЁАЮоЁБЃЉЮЃЯеЃЛ
ЃЈ2ЃЉМДНЋВЮМгжаПМЕФСНУћЭЌбЇЕФЖдЛАЃКМзЭЌбЇЃКЁАЮве§ГЃЧщПіЯТдкдЫЖЏЪБЫљФмГаЪмЕФУПЗжаФЬјЕФзюИпДЮЪ§ЪЧ164ДЮЁБЃЌввЭЌбЇЃКЁАЮве§ГЃЧщПіЯТдкдЫЖЏЪБЫљФмГаЪмЕФУПЗжаФЬјЕФзюИпДЮЪ§ВХ156ДЮЁБЃЎЧыФуХаЖЯМзввСНУћЭЌбЇЫЕФЫЕЗЈЪЧДэЮѓЕФЃПВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєвЛИіШЫЕФФъСфгЩ![]() БфЮЊ
БфЮЊ![]() ЃЈ
ЃЈ![]() ЮЊе§ећЪ§ЃЉЃЌЗЂЯже§ГЃЧщПіЯТетИіШЫдкдЫЖЏЪБЫљФмГаЪмЕФУПЗжаФЬјЕФзюИпДЮЪ§МѕЩйСЫ12ЃЌгУСаЗНГЬЕФЗНЗЈШЗЖЈ
ЮЊе§ећЪ§ЃЉЃЌЗЂЯже§ГЃЧщПіЯТетИіШЫдкдЫЖЏЪБЫљФмГаЪмЕФУПЗжаФЬјЕФзюИпДЮЪ§МѕЩйСЫ12ЃЌгУСаЗНГЬЕФЗНЗЈШЗЖЈ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌЕуEЪЧCDЩЯвЛЕуЃЈВЛгыCЃЌDСНЕужиКЯЃЉЃЌСЌНгBEЃЌЙ§ЕуCзїCHЁЭBEгкЕуFЃЌНЛЖдНЧЯпBDгкЕуGЃЌНЛADБпгкЕуHЃЌСЌНгGEЃЌ
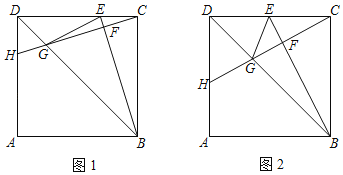
ЃЈ1ЃЉЧѓжЄЃКЁїDHCЁеЁїCEBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуEЪЧCDЕФжаЕуЃЌЕБBEЃН8ЪБЃЌЧѓЯпЖЮGHЕФГЄЃЛ
ЃЈ3ЃЉЩше§ЗНаЮABCDЕФУцЛ§ЮЊS1ЃЌЫФБпаЮDEGHЕФУцЛ§ЮЊS2ЃЌЕБ![]() ЕФжЕЮЊ
ЕФжЕЮЊ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЮЊЁЁ ЁЁЃЎ
ЕФжЕЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇЯАвЛЖЈвЊНВОПЗНЗЈЃЌБШШчгааЇЕФдЄЯАПЩДѓЗљЬсИпЬ§ПЮаЇТЪЃЎОХФъМЖЃЈ1ЃЉАрбЇЯАаЫШЄаЁзщЮЊСЫСЫНтШЋаЃОХФъМЖбЇЩњЕФдЄЯАЧщПіЃЌЖдИУаЃОХФъМЖбЇЩњУПЬьЕФПЮЧАдЄЯАЪБМфЃЈЕЅЮЛЃК![]() ЃЉНјааСЫГщбљЕїВщЃЎВЂНЋГщВщЕУЕНЕФЪ§ОнЗжГЩ5зщЃЌЯТУцЪЧЮДЭъГЩЕФЦЕЪ§ЁЂЖйТЪЗжВМБэКЭЦЕЪ§ЗжВМЩШаЮЭМЃЎ
ЃЉНјааСЫГщбљЕїВщЃЎВЂНЋГщВщЕУЕНЕФЪ§ОнЗжГЩ5зщЃЌЯТУцЪЧЮДЭъГЩЕФЦЕЪ§ЁЂЖйТЪЗжВМБэКЭЦЕЪ§ЗжВМЩШаЮЭМЃЎ
зщБ№ | ПЮЧАдЄЯАЪБМф | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
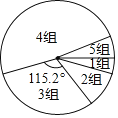
ЧыИљОнЭМБэжаЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщЕФбљБОШнСПЮЊ ЃЌБэжаЕФ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЪдМЦЫуЕк4зщШЫЪ§ЫљЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИУаЃОХФъМЖЦфга1000УћбЇЩњЃЌЧыЙРМЦетаЉбЇЩњжаУПЬьПЮЧАдЄЯАЪБМфВЛЩйгк![]() ЕФбЇЩњШЫЪ§ЃЎ
ЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФВМДќжазАгаЯрЭЌЕФШ§ИіаЁЧђЃЌЦфЩЯУцЗжБ№БъзЂЪ§зж1ЁЂ2ЁЂ3ЁЂЃЌЯжДгжаШЮвтУўГівЛИіаЁЧђЃЌНЋЦфЩЯУцЕФЪ§зжзїЮЊЕуMЕФКсзјБъЃЛНЋЧђЗХЛиДќжаНСдШЃЌдйДгжаШЮвтУўГівЛИіаЁЧђЃЌНЋЦфЩЯУцЕФЪ§зжзїЮЊЕуMЕФзнзјБъЃЎ
ЃЈ1ЃЉЧѓЕуMдкжБЯпy=xЩЯЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓЕуMЕФКсзјБъгызнзјБъжЎКЭЪЧХМЪ§ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпlЃК![]() гы
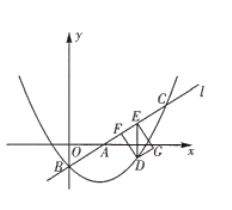
гы![]() жсНЛгкЕуAЃЌНЋжБЯпlШЦЕуAЫГЪБеыа§зЊ75ЁуКѓЃЌЫљЕУжБЯпЕФНтЮіЪНЮЊЃЈ ЃЉ
жсНЛгкЕуAЃЌНЋжБЯпlШЦЕуAЫГЪБеыа§зЊ75ЁуКѓЃЌЫљЕУжБЯпЕФНтЮіЪНЮЊЃЈ ЃЉ
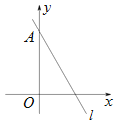
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЧв
ЕФжБОЖЃЌЧв![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌНЋЛЁ
ЩЯвЛЕуЃЌНЋЛЁ![]() бижБЯп
бижБЯп![]() ЗелЃЌЪЙЗелКѓЕФдВЛЁЧЁКУОЙ§дВаФ
ЗелЃЌЪЙЗелКѓЕФдВЛЁЧЁКУОЙ§дВаФ![]() ЃЌдђ
ЃЌдђ
ЃЈ1ЃЉ![]() ЕФГЄЪЧ_________ЃЎ
ЕФГЄЪЧ_________ЃЎ
ЃЈ2ЃЉСгЛЁ![]() ЕФГЄЪЧ__________ЃЎ
ЕФГЄЪЧ__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯп![]() гыЫЋЧњЯп
гыЫЋЧњЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌгызјБъжсЗжБ№НЛгкЕу
ЃЌгызјБъжсЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
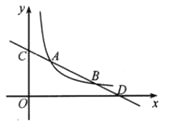
ЃЈ1ЃЉЧѓжБЯп![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉдк![]() жсЩЯЧѓГіЕу
жсЩЯЧѓГіЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЮЊЖЅЕуЕФШ§НЧаЮгы
ЮЊЖЅЕуЕФШ§НЧаЮгы![]() ЯрЫЦЃЎ
ЯрЫЦЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com