
分析 (1)由方程有两个整数根,可得△=16m+20=4(4m+5),即可得4m+5是平方数,又由m是满足12<m<20的整数,即可求得答案;
(2)由关于x的一元二次方程x2-(2m-1)x+m2-1=0②与x2-4mx+4m2-4m-5=0①的根都是整数,首先易得-$\frac{5}{4}$≤m≤$\frac{5}{4}$,又由m取整数,即可求得答案.
解答 解:(1)∵关于x的一元二次方程x2-4mx+4m2-4m-5=0方程有两个整数根,
∴△=b2-4ac=(-4m)2-4×1×(4m2-4m-5)=16m+20=4(4m+5),
∵方程有两个整数根,
∴4m+5是平方数,
∵m是满足12<m<20的整数,
∴m=19;
(2)∵△1=b2-4ac=[-(2m-1)]2-4×1×(m2-1)=-4m+5≥0,
∴m≤$\frac{5}{4}$,
∵△2=b2-4ac=16m+20≥0,
∴m≥-$\frac{5}{4}$,
∴-$\frac{5}{4}$≤m≤$\frac{5}{4}$,
∴m=-1,0,1,
∵根都是整数,
∴m=±1.
点评 此题考查了根的判别式以及完全平方数.注意根据题意得到△=16m+20=4(4m+5),继而4m+5是平方数是解此题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
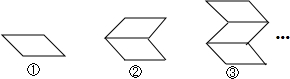
| 图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
| 火柴棒的根数 | 4 | 7 | 10 | 13 | 16 | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
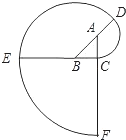 如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为( )
如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为( )| A. | $\frac{12+7\sqrt{2}}{4}π$ | B. | $\frac{7+4\sqrt{2}}{4}π$ | C. | $\frac{5+3\sqrt{2}}{4}π$ | D. | $\frac{10+5\sqrt{2}}{4}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
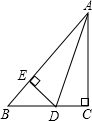 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BC=9,BE=3,则△BDE的周长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BC=9,BE=3,则△BDE的周长为( )| A. | 15 | B. | 12 | C. | 9 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com