
分析 分两种情况讨论:①若∠A<90°;②若∠A>90°;先求出顶角∠BAC,即可求出底角的度数.
解答 解:分两种情况讨论:
①若∠A<90°,如图1所示: ∵BD⊥AC,
∵BD⊥AC,
∴∠A+∠ABD=90°,
∵∠ABD=50°,
∴∠A=90°-50°=40°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-40°)=70°;
②若∠A>90°,如图2所示: 同①可得:∠DAB=90°-50°=40°,
同①可得:∠DAB=90°-50°=40°,
∴∠BAC=180°-40°=140°,
∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-140°)=20°;
综上所述:等腰三角形底角的度数为70°或20°
点评 本题考查了等腰三角形的性质以及余角和邻补角的定义;注意分类讨论方法的运用,避免漏解.


科目:初中数学 来源: 题型:填空题
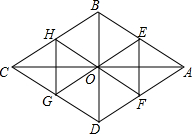 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
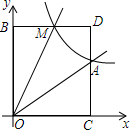 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7200(1+x)2=8400 | B. | 7200(1+x2)=8400 | C. | 7200(x2+x)=8400 | D. | 7200(1+x)=8400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
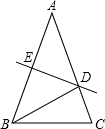 如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com