【题目】如图，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上．若∠BAD=120°，则弧BC的长度等于 .
【答案】
【解析】解答: ∵菱形ABCD中，AB=BC，
又∵AC=AB，
∴AB=BC=AC，即△ABC是等边三角形．
∴∠BAC=60°，
∴弧BC的长是： 
故答案是：
本题考查了弧长公式，理解B，C两点恰好落在扇形AEF的弧EF上，即B、C在同一个圆上，得到△ABC是等边三角形是关键．
【考点精析】根据题目的已知条件，利用菱形的性质和弧长计算公式的相关知识可以得到问题的答案，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的．
科目：初中数学 来源： 题型：
【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球（除颜色外其余均相同）．其中白球、黄球各1个，若从中任意摸出一个球是白球的概率是 
．
（1）求暗箱中红球的个数．
（2）先从暗箱中任意摸出一个球记下颜色后放回，再从暗箱中任意摸出一个球，求两次摸到的球颜色不同的概率（用树形图或列表法求解）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数填入相应的括号内：11，－
，6.5，－8，3
，0，1，－1，－3.14.
(1)正数集合：{ …}；(2)负数集合：{ …}；
(3)整数集合：{ …}；(4)正整数集合：{ …}；
(5)负整数集合：{ …}；(6)分数集合：{ …}；
(7)正分数集合：{ …}；(8)负分数集合：{ …}；
(9)有理数集合：{ …}．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，大、中、小三个圆圈分别表示有理数集合、整数集合、自然数集合，把这三个圆圈如图②所示叠放在一起，形成大圆环A和小圆环B，则小圆环B表示的是负整数集合．请你把－20，0，3.14，－
，5填入图②相应的位置中，并写出大圆环A所表示集合的名称．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出300元之后，超出部分按原价8折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价8.5折优惠．设顾客预计累计购物
元(
)．
(1)请用含
的代数式分别表示顾客在两家超市购物所付的费用；
(2)李明准备购买500元的商品，你认为他应该去哪家超市？请说明理由；
(3)计算一下，李明购买多少元的商品时，到两家超市购物所付的费用一样？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，C为线段AB延长线上一点，D为线段BC上一点，CD＝2BD，E为线段AC上一点，CE＝2AE
(1)若AB＝18，BC＝21，求DE的长；
(2)若AB＝a，求DE的长；(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍，则
的值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=3，AC=4，BC=5，D、E分别是AC、AB的中点，则以DE为直径的圆与BC的位置关系是（ ）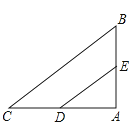
A.相切
B.相交
C.相离
D.无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图17－Z－10是由边长为1的小正方形组成的网格．
(1)求四边形ABCD的面积；
(2)你能判断AD与CD的位置关系吗？说出你的理由．
图17－Z－10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
