
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
![]()
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为 .
的值为 .
【答案】(1)12;(2)![]() ;(3)
;(3) ![]() .
.
【解析】
(1)利用CD=2BD,CE=2AE,得出AE=![]() AC=
AC=![]() (AB+BC),进一步利用BE=AB-AE,DE=BE+BD得出结论即可;
(AB+BC),进一步利用BE=AB-AE,DE=BE+BD得出结论即可;
(2)利用(1)的计算过程即可推出;
(3)图中所有线段有AE、AB、AD、AC、EB、ED、EC、BD、BC、DC共10条,求出所有线段的和用AC表示即可.
解:(1)∵CD=2BD,BC=21,
∴BD=![]() BC=7,
BC=7,
∵CE=2AE,AB=18,
∴AE=![]() AC=
AC=![]() (AB+BC)=
(AB+BC)=![]() ×(18+21)=13,
×(18+21)=13,
∴BE=AB﹣AE=18﹣13=5,
∴DE=BE+BD=5+7=12;
(2)∵CD=2BD,
∴BD=![]() BC,
BC,
∵CE=2AE,AB=a,
∴AE=![]() AC,
AC,
∴BE=AB﹣AE=AB﹣![]() AC,
AC,
∴DE=BE+BD=AB﹣![]() AC+
AC+![]() BC=AB﹣
BC=AB﹣![]() (AC﹣BC)=AB﹣
(AC﹣BC)=AB﹣![]() AB=
AB=![]() AB,
AB,
∵AB=a,
∴DE=![]() a;
a;
(3)设CD=2BD=2x,CE=2AE=2y,
则BD=x,AE=y,
所有线段和AE+AB+AD+AC+EB+ED+EC+BD+BC+DC=4y+3(2y﹣3x)+2x+2x+3(2y﹣3x)+2x+2x+2x+2x+2x=7(y+2y﹣3x+x),
y=2x,
则AD=y+2y﹣3x+x=3y﹣2x=4x,AC=3y=6x,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求弧FG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y=![]() x+3的图象经过点B、C.
x+3的图象经过点B、C.

(1)点C的坐标为_____,点B的坐标为_____;
(2)如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
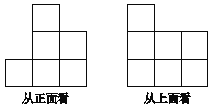
【题目】用大小相同的小立方块搭成一个几何体,使得从正面和上面看到的几何体的形状图如图19所示.
(1)这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
(2)画出这两种情况下从左面看到的几何体的形状图.(各画出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
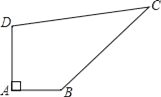
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com