
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为( ) 
A.3 ![]()
B.2 ![]()
C.2 ![]()
D.2 ![]()
【答案】B
【解析】解:过点E作EM⊥BC于M,交BF于N, 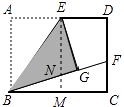
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
∵∠ENG=∠BNM,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴CM=DE,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM= ![]() CF=
CF= ![]() ,
,
∴NG= ![]() ,
,
∵BG=AB=CD=CF+DF=3,
∴BN=BG﹣NG=3﹣ ![]() =
= ![]() ,
,
∴BF=2BN=5,
∴BC= ![]() =
= ![]() =2
=2 ![]() .
.
故选B.
首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=3,继而求得BF的值,又由勾股定理,即可求得BC的长.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表,从下表可知:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
下列说法错误的是( )。
A.抛物线与x轴的另一个交点为(3,0);
B.函数的最大值为6;
C.抛物线的对称轴是直线x=0.5;
D.在对称轴的左侧,y随x的增大而增大。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 . 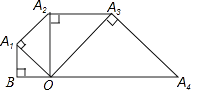
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.) 
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值.
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,ADBC,AC、BD相交于点O,AB⊥AC,AD=CD,AB=3,BC=5.求: 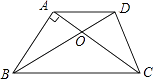
(1)tan∠ACD的值;
(2)梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=2,则EC的长度为( ) 
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G. 
(1)求证:BF=AC;
(2)求证:CE= ![]() BF.
BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ![]() ),则点C的坐标为( )
),则点C的坐标为( ) 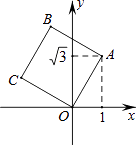
A.(﹣ ![]() ,1)
,1)
B.(﹣1, ![]() )
)
C.( ![]() ,1)
,1)
D.(﹣ ![]() ,﹣1)
,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com