
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G. 
(1)求证:BF=AC;
(2)求证:CE= ![]() BF.
BF.
【答案】
(1)证明:∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.
∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
在Rt△DFB和Rt△DAC中,
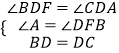 ,
,
∴Rt△DFB≌Rt△DAC(AAS),
∴BF=AC
(2)证明:∵BE平分∠ABC,
∴∠ABE=∠CBE.
在Rt△BEA和Rt△BEC中,
 ,
,
∴Rt△BEA≌Rt△BEC(ASA).
∴CE=AE= ![]() AC,
AC,
又∵BF=AC,
∴CE= ![]() BF
BF
【解析】(1)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;(2)推出∠AEB=∠CEB,∠ABE=∠CBE,根据ASA证出△AEB≌△CEB,推出AE=CE即可.


科目:初中数学 来源: 题型:
【题目】黄麻中学为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元,已知学校用12000元购买的科普类图书的本数与用5000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为( ) 
A.3 ![]()
B.2 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为 ![]() ,则a的值是( )
,则a的值是( ) 
A.4
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,1),B(1,4),若反比例函数y= ![]() 与线段AB有公共点时,k的取值范围是( )
与线段AB有公共点时,k的取值范围是( )
A.﹣2≤k≤4
B.k≤﹣2或k≥4
C.﹣2≤k<0或k≥4
D.﹣2≤k<0或0<k≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种新型节能电水壶并加以销售,现准备在甲城市和乙城市两个不同地方按不同销售方案进行销售,以便开拓市场. 若只在甲城市销售,销售价格为y(元/件)、月销量为x(件),y是x的一次函数,如表,
月销量x(件) | 1500 | 2000 |
销售价格y(元/件) | 185 | 180 |
成本为50元/件,无论销售多少,每月还需支出广告费72500元,设月利润为W甲(元)
(利润=销售额﹣成本﹣广告费).
若只在乙城市销售,销售价格为200元/件,受各种不确定因素影响,成本为a元/件(a为常数,40≤a≤70),当月销量为x(件)时,每月还需缴纳 ![]() x2元的附加费,设月利润为W乙(元)(利润=销售额﹣成本﹣附加费).
x2元的附加费,设月利润为W乙(元)(利润=销售额﹣成本﹣附加费).
(1)当x=1000时,y甲=元/件,w甲=元;
(2)分别求出W甲 , W乙与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在甲城市销售的月利润最大?若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同,求a的值;
(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在甲城市还是在乙城市销售才能使所获月利润较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE. 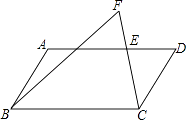
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中:
①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0.
正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com