
【题目】如图,点E是矩形ABCD的对角线BD上的一点,且BE=BC,AB=3,BC=4,点P为直线EC上的一点,且PQ⊥BC于点Q,PR⊥BD于点R.

(1)①如图1,当点P为线段EC中点时,易证:PR+PQ= ![]() (不需证明).②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(不需证明).②如图2,当点P为线段EC上的任意一点(不与点E、点C重合)时,其它条件不变,则①中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(2)如图3,当点P为线段EC延长线上的任意一点时,其它条件不变,则PR与PQ之间又具有怎样的数量关系?请直接写出你的猜想.
【答案】(1)成立,理由见解析;(2)PR﹣PQ=![]()
【解析】
试题(1)②连接BP,过C点作CK⊥BD于点K.根据矩形的性质及勾股定理求出BD的长,根据三角形面积相等可求出CK的长,最后通过等量代换即可证明;
(2)图3中的结论是PR﹣PQ=![]() .
.
试题解析:解:(1)②图2中结论PR+PQ=![]() 仍成立.
仍成立.
证明:连接BP,过C点作CK⊥BD于点K.
∵四边形ABCD为矩形,∴∠BCD=90°.又∵CD=AB=3,BC=4,∴BD=![]() =
=![]() =5.
=5.
∵S△BCD=![]() BCCD=
BCCD=![]() BDCK,∴3×4=5CK,∴CK=
BDCK,∴3×4=5CK,∴CK=![]() .
.
∵S△BCE=![]() BECK,S△BEP=
BECK,S△BEP=![]() PRBE,S△BCP=
PRBE,S△BCP=![]() PQBC,且S△BCE=S△BEP+S△BCP,∴
PQBC,且S△BCE=S△BEP+S△BCP,∴![]() BECK=
BECK=![]() PRBE+
PRBE+![]() PQBC.又∵BE=BC,∴
PQBC.又∵BE=BC,∴![]() CK=
CK=![]() PR+
PR+![]() PQ,∴CK=PR+PQ.又∵CK=
PQ,∴CK=PR+PQ.又∵CK=![]() ,∴PR+PQ=
,∴PR+PQ=![]() ;
;
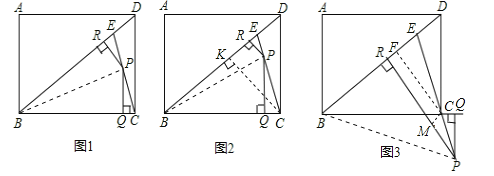
(2)过C作CF⊥BD交BD于F,作CM⊥PR交PR于M,连接BP,S△BPE﹣S△BCP=S△BEC,S△BEC是固定值,BE=BC为两个底,PR,PQ 分别为高,图3中的结论是PR﹣PQ=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣ ![]() ),(
),( ![]() )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 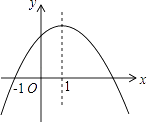
A.①②
B.②③
C.②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
①甲车提速后的速度是60千米/时;
②乙车的速度是96千米/时;
③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市乙车已返回A市2小时10分钟.
其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
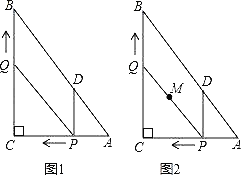
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
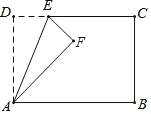
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA. 
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com