Question

【题目】如图是二次函数y=ax2+bx+c的图象，其对称轴为x=1，下列结论：①abc＞0；②2a+b=0；③4a+2b+c＜0；④若（﹣ ），（ ）是抛物线上两点，则y1＜y2其中结论正确的是（ ）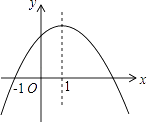

A.①②
B.②③
C.②④
D.①③④

Answer 1

【答案】C
【解析】解：∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴为直线x=﹣ =1，
∴b=﹣2a＞0，
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
∴abc＜0，所以①错误；
∵b=﹣2a，
∴2a+b=0，所以②正确；
∵抛物线与x轴的一个交点为（﹣1，0），抛物线的对称轴为直线x=1，
∴抛物线与x轴的另一个交点为（3，0），
∴当x=2时，y＞0，
∴4a+2b+c＞0，所以③错误；
∵点（﹣ ）到对称轴的距离比点（ ）对称轴的距离远，
∴y1＜y2 ， 所以④正确．
故选C．
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．