
【题目】在边长为2的正方形ABCD中,点P、Q分别是边AB、BC上的两个动点(与点A、B、C不重合),且始终保持BP=BQ,AQ⊥QE,QE交正方形外角平分线CE于点E,AE交CD于点F,连结PQ.
(1)求证:△APQ≌△QCE;
(2)求∠QAE的度数;
(3)设BQ=x,当x为何值时,QF∥CE,并求出此时△AQF的面积.

【答案】(1)证明见解析;(2)45°;(3)当x=-2+2![]() 时,S=-4+4
时,S=-4+4![]() .
.
【解析】
试题(1)判断出△PBQ是等腰三角形,然后求出∠APQ=∠QCE=135°,再根据同角的余角相等求出∠PAQ=∠CQE,再求出AP=CQ,然后利用“角边角”证明即可;
(2)根据全等三角形对应边相等可得AQ=EQ,判断出△AQE是等腰三角形,再根据等腰三角形的性质解答;
(3)把△ABQ绕点A逆时针旋转90°得到△ADG,求出∠GAF=45°,从而得到∠GAF=∠QAF,再利用“边角边”证明△AQF和△AGF全等,根据全等三角形的对应边相等可得QF=GF,再根据两直线平行,同位角相等求出∠CQF=45°,然后求出CQ=CF,分别用x求出CQ、CF,利用勾股定理列式求出QF,然后列出方程求出x,再求出△AGF的面积,即为△AQF的面积.
试题解析:(1)∵ 四边形ABCD是正方形,
∴ AB=BC,∠B=∠BCD=∠DCM=90°,
∵ BP=BQ,
∴ △PBQ是等腰直角三角形,AP=QC,
∴ ∠BPQ=45°,
∴ ∠APQ=135°
∵ CE平分∠DCM,
∴ ∠DCE=∠ECM=45°,
∴ ∠QCE=135°,
∴ ∠APQ=∠QCE=135°,
∵ AQ⊥QE,即 ∠AQE=90°,
∴ ∠AQB+∠CQE=90°.
∵ ∠AQB+∠BAQ=90°.
∴ ∠BAQ=∠CQE.
∴ △APQ≌△QCE(ASA).
(2)由(1)知△APQ≌△QCE.∴ QA=QE.
∵ ∠AQE=90°,
∴ △AQE是等腰直角三角形,∴ ∠QAE=45°
(3)连结AC,若QF∥CE,则∠FQC=∠ECM=45°.
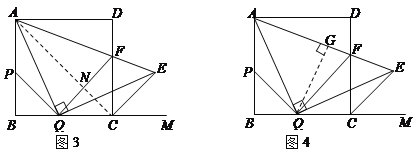
∴ △QCF是等腰直角三角形,∴ CF=CQ=2-x, ∴ DF=BQ=x.
∵ AB=AD,∠B=∠D=90°,
∴ △ABQ≌△ADF(SAS).
∴ AQ=AF,∠QAB=∠DAF=22.5°,
∴ AC垂直平分QF,
∴ ∠QAC=∠FAC=∠QAB=∠FAD=22.5°, FQ=2QN,
∴ FQ=2BQ=2x.
在Rt△QCF中,根据勾股定理,得(2-x)2+(2-x)2=(2x)2.
解这个方程,得 x1=-2+2![]() , x2=-2-2
, x2=-2-2![]() (舍去).
(舍去).
∴ 当x=-2+2![]() 时,QF∥CE.
时,QF∥CE.
此时,S△QCF=S△QEF,
∴ S△QCF+ S△AQF=S△QEF+ S△AQF= S△AQE=![]() AQ2,
AQ2,
∴ S△AQF= S△AQE- S△QCF=![]() AQ2-
AQ2-![]() CQ2=
CQ2=![]() (AQ2-CQ2)
(AQ2-CQ2)
=![]() [(x2+22)-(2-x)2]=
[(x2+22)-(2-x)2]=![]() ·4x=2x=-4+4
·4x=2x=-4+4![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机从箱子里取出1个球,则取出黄球的概率是多少?
(2)随机从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示出所有可能出现的结果,并求两次取出的都是白色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣ ![]() ),(
),( ![]() )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 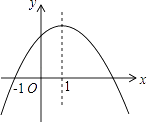
A.①②
B.②③
C.②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
问题:如图1,已知EF为△ABC的中位线,M是边BC上一动点,连接AM交EF于点P,那么动点P为线段AM中点.
理由:∵线段EF为△ABC的中位线,∴EF∥BC,
由平行线分线段成比例得:动点P为线段AM中点.
由此你得到动点P的运动轨迹是: .
(2)知识应用:
如图2,已知EF为等边△ABC边AB、AC上的动点,连结EF;若AF=BE,且等边△ABC的边长为8,求线段EF中点Q的运动轨迹的长.
(3)拓展提高:
如图3,P为线段AB上一动点(点P不与点A、B重合),在线段AB的同侧分别作等边△APC和等边△PBD,连结AD、BC,交点为Q.
①求∠AQB的度数;
②若AB=6,求动点Q运动轨迹的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=8 ![]() ,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= .
,AD=10,点E是CD中点,将这张纸片依次折叠两次;第一次折叠纸片使点A与点E重合,如图2,折痕为MN,连接ME、NE;第二次折叠纸片使点N与点E重合,如图3,点B落到B′处,折痕为HG,连接HE,则tan∠EHG= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
①甲车提速后的速度是60千米/时;
②乙车的速度是96千米/时;
③乙车返回时y与x的函数关系式为y=﹣96x+384;
④甲车到达B市乙车已返回A市2小时10分钟.
其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
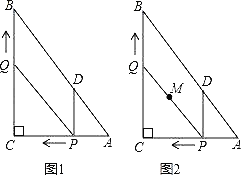
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com