
����Ŀ����֪����x��һԪ���η���x2+2x+ ![]() =0��ʵ������kΪ��������
=0��ʵ������kΪ��������
��1����k��ֵ��
��2�����˷��������������������ʱ��������x�Ķ��κ���y=x2+2x+ ![]() ��ͼ������ƽ��9����λ����ƽ�ƺ��ͼ��ı���ʽ��
��ͼ������ƽ��9����λ����ƽ�ƺ��ͼ��ı���ʽ��
��3���ڣ�2���������£�ƽ�ƺ�Ķ��κ�����ͼ����x�ύ�ڵ�A��B����A�ڵ�B��ࣩ��ֱ��y=kx+b��k��0������B�����������ߵ���һ������ΪC��ֱ��BC�Ϸ������������߶�BC����µ�ͼ������ͼ�����Сֵ���ک�5ʱ����k��ȡֵ��Χ��
���𰸡�
��1��
�⣺�߹���x��һԪ���η���x2+2x+ ![]() =0��ʵ������
=0��ʵ������
���=b2��4ac=4��4�� ![]() ��0��
��0��
��k��1��2��
��k��3��
��k��������
��k��ֵ��1��2��3��
��2��
�⣺�߷����������������������
��k=1ʱ��x2+2x=0���������⣬��ȥ��
��k=2ʱ��x2+2x+ ![]() =0��
=0��
���̵ĸ������������������⣬��ȥ��
��k=3ʱ��x2+2x+1=0��
��ã�x1=x2=��1���������⣬
��k=3��
��y=x2+2x+1��
��ƽ�ƺ��ͼ��ı���ʽy=x2+2x+1��9=x2+2x��8��
��3��
�⣺��y=0��x2+2x��8=0��
��x1=��4��x2=2��
����x�ύ�ڵ�A��B����A�ڵ�B��ࣩ��
��A����4��0����B��2��0����
��ֱ��l��y=kx+b��k��0��������B��
�ຯ����ͼ����ͼ��ʾ������C�������߶Գ������ʱ���º�������Сֵ�п��ܴ��ک�5��
��y=��5����x2+2x��8=��5��
��ã�x1=��3��x2=1�����������⣬��ȥ����
�������߾����㣨��3����5����
��ֱ��y=kx+b��k��0�������㣨��3����5������2��0��ʱ��
�����k=1��
��ͼ���֪����0��k��1ʱ�º�������Сֵ���ک�5��
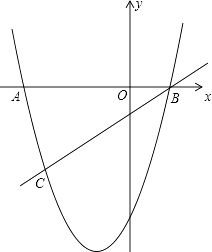
����������1�����ݷ�����ʵ�����ɵá���0�����k��ȡֵ��Χ��Ȼ�����kΪ�������ó�k��ֵ����2�����ݷ�������������������������жϣ��ó�k=3��Ȼ��ó���������ʽ��������ƽ�Ƶ��������ƽ�ƺ��ͼ��ı���ʽ����3����y=0���ó�A��B�����꣬����ͼ��Ȼ������º�������Сֵ���ک�5�����C�����꣬Ȼ�����B��C�����������ʱk��ֵ�����ɵó�k��ȡֵ��Χ��


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��2��k+1��x+k2=0������ʵ����x1��x2 ��
��1����k��ȡֵ��Χ��
��2����x1+x2=3x1x2��6����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��DE��AC��DF��AC=DF�����������������ж���ABC�ա�DEF������������

A. AB=DE B. ��B=��E C. EF=BC D. EF��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������������װ�лơ��ס��ڸ�һ�������dz�����ɫ֮��û����������
��1�������������ȡ��1������ȡ������ĸ����Ƕ��٣�
��2�������������ȡ��1���Żؽ�����ȡ�ڶ����������û���״ͼ���б��ķ�����ʾ�����п��ܳ��ֵĽ������������ȡ���Ķ��ǰ�ɫ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x�ĺ���y=ax2+��a+2��x+a+1��ͼ����x��ֻ��һ�������㣬��ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣮ֱ��y=kx+b��������y=mx2�� ![]() x+nͬʱ����A��0��3����B��4��0����
x+nͬʱ����A��0��3����B��4��0����
��1����m��n��ֵ��
��2����M�Ƕ��κ���ͼ����һ�㣬����M��AB�·�������M��MN��x�ᣬ��AB���ڵ�N����x�ύ�ڵ�Q����MN�����ֵ��
��3���ڣ�2���������£��Ƿ���ڵ�N��ʹ��AOB�͡�NOQ���ƣ������ڣ����N�����꣬�����ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BOC=9�㣬��A��OB�ϣ���OA=1��������Ҫ��ͼ��
��AΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A1���õ�1���߶�AA1������A1ΪԲ�ģ�1Ϊ�뾶���һ�����OB�ڵ�A2���õ�2���߶�A1A2������A2ΪԲ�ģ�1Ϊ�뾶���һ�����OC�ڵ�A3���õ�3���߶�A2A3������������ȥ��ֱ���õ�n���߶Σ�֮��Ͳ����ٻ�������Ҫ����߶��ˣ���n=______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��ͼ����Գ���Ϊx=1�����н��ۣ���abc��0����2a+b=0����4a+2b+c��0���������� ![]() ������
������ ![]() ���������������㣬��y1��y2���н�����ȷ���ǣ� ��
���������������㣬��y1��y2���н�����ȷ���ǣ� �� 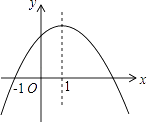
A.�٢�
B.�ڢ�
C.�ڢ�
D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�е�B�е�·��Ϊ260ǧ�ף��׳���A��ǰ��B���������ʣ���ʻ2Сʱ��M���������ֹ��ϣ�����֪ͨ������Ա���ҳ���A�и���ά�ޣ�֪ͨʱ����Բ��ƣ����ҳ�����M�غ��־���20�����ü׳�����ԭ��ԭ·����A�У�ͬʱ�׳���ԭ��1.5�����ٶ�ǰ��B�У���ͼ��������A�е�·��y��ǧ�ף���׳�����ʱ��x��Сʱ��֮��ĺ���ͼ����������˵����
�ټ׳����ٺ���ٶ���60ǧ��/ʱ��
���ҳ����ٶ���96ǧ��/ʱ��
���ҳ�����ʱy��x�ĺ�����ϵʽΪy=��96x+384��
�ܼ׳�����B���ҳ��ѷ���A��2Сʱ10���ӣ�
������ȷ�ĸ����ǣ�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com