
分析 (1)根据一次函数的性质可知:m+2>0;
(2)根据一次函数的性质进行解答即可;
(3)把x=0,y=0代入解析式解答即可;
(4)根据函数的图象经过第一、二、三象限列出不等式解答即可.
解答 解:(1)∵函数y的值随x值的增大而增大
∴m+2>0,
∴m>-2;
(2)∵函数的图象与y轴的交点在x轴的下方,
∴2-n<0,m+2≠0
∴n>2,m≠-2;
(3)∵函数的图象与坐标轴交于原点,
∴2-n=0,m+2≠0,
∴n=2,m≠-2,
(4)∵函数的图象经过第一、二、三象限,
∴m+2>0,2-n>0,
∴n<2,m>-2.
点评 本题主要考查一次函数的图象与系数的关系,当x的系数大于0时,函数y随自变量x的增大而增大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④△CGF是等边三角形.其中正确结论的个数( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
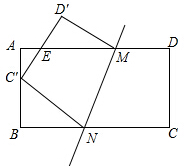 如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.
如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com