
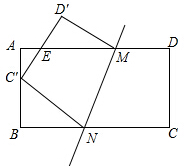
 如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.
如图,把矩形纸片ABCD折叠,使点C落在AB边上的点C′处(与点A,B不重合),点D落在D′处,C′D′交AD于点E,折痕为MN.分析 (1)设BC′=x时,△NBC′≌△C′AE,先根据全等三角形的性质得出BN=AC′=7-x,于是NC=BC-BN=2+x,再由折叠的性质得到NC′=NC=2+x,然后在Rt△BNC′中利用勾股定理列出方程(2+x)2=x2+(7-x)2,解方程即可;
(2)设BC′=x时,△NBC′≌△C′AE,先根据全等三角形的性质得出BN=AC′=AB-BC′=1-x,验算NC=BC-BN=x,再由折叠的性质得到NC′=NC=x,然后在Rt△BNC′中根据斜边最长得出NC′>BC′,这与NC′=BC′=x矛盾,于是得出结论:如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
解答 解:(1)设BC′=x时,△NBC′≌△C′AE,则BN=AC′=AB-BC′=7-x,NC=BC-BN=9-(7-x)=2+x,
∵把矩形ABCD折叠,使点C落在AB上的C′处,折痕为MN,
∴NC′=NC=2+x.
在Rt△BNC′中,∵∠B=90°,
∴NC′2=BC′2+BN2,
∴(2+x)2=x2+(7-x)2,
解得x1=3,x2=15,
∵15>AB,舍去,故x=3,即当点C′在AB上距离点B3个单位时,可使△NBC′≌△C′AE;
(2)如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
理由如下:
设BC′=x时,△NBC′≌△C′AE,则BN=AC′=AB-BC′=1-x,NC=BC-BN=1-(1-x)=x.
∵把矩形ABCD折叠,使点C落在AB上的C′处,折痕为MN,
∴NC′=NC=x.
在Rt△BNC′中,∵∠B=90°,
∴NC′>BC′,
而NC′=BC′=x,
∴如果AB=BC=1,使△NBC′≌△C′AE的C′不存在.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.同时考查了直角三角形的性质及一元二次方程的解法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
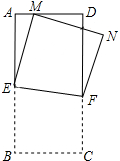 如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).
如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com