
【题目】阅读下列材料并解决有关问题:我们知道|x|= 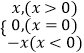 ,
,
所以当x>0时, ![]() =
= ![]() =1; 当x<0时,
=1; 当x<0时, ![]() =
= ![]() =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时, ![]() +
+ ![]() =;
=;
(2)已知a,b是有理数,当abc≠0时, ![]() +
+ ![]() +
+ ![]() =;
=;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 ![]() +
+ ![]() +
+ ![]() = .
= .
【答案】
(1)解:已知a,b是有理数,当ab≠0时,
①a<0,b<0, ![]() +
+ ![]() =﹣1﹣1=﹣2;
=﹣1﹣1=﹣2;
②a>0,b>0, ![]() +
+ ![]() =1+1=2;
=1+1=2;
③a、b异号, ![]() +
+ ![]() =0.
=0.
故 ![]() +
+ ![]() =±2或0
=±2或0
(2)[ "解:已知a,b是有理数,当abc≠0时,
①a<0,b<0,c<0, ![]() +
+ ![]() +
+ ![]() =﹣1﹣1﹣1=﹣3;
=﹣1﹣1﹣1=﹣3;
②a>0,b>0,c>0, ![]() +
+ ![]() +
+ ![]() =1+1+1=3;
=1+1+1=3;
③a、b、c两负一正, ![]() +
+ ![]() +
+ ![]() =﹣1﹣1+1=﹣1;
=﹣1﹣1+1=﹣1;
④a、b、c两正一负, ![]() (3)解:已知a,b,c是有理数,a+b+c=0,abc<0,
(3)解:已知a,b,c是有理数,a+b+c=0,abc<0,
则b+c=﹣a,a+c=﹣b,a+b=﹣c,a、b、c两正一负,
则 ![]() +
+ ![]() +
+ ![]() ═﹣
═﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =1﹣1﹣1=﹣1.
=1﹣1﹣1=﹣1.
故答案为:±2或0;±1或±3;﹣1
【解析】(1)分3种情况讨论即可求解;(2)分4种情况讨论即可求解;(3)根据已知得到b+c=﹣a,a+c=﹣b,a+b=﹣c,a、b、c两正一负,进一步计算即可求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=90°,AC=BD,AC⊥BD,若AB=4, AD=5,则DC的长 ( ).

A. 7 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
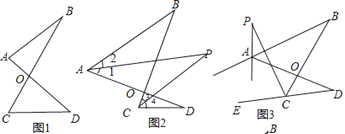
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
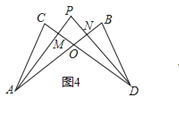
【拓展延伸】
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠1与∠2互为余角,∠1与∠3互为补角,那么下列结论: ①∠3﹣∠2=90° ②∠3+∠2=270°﹣2∠1 ③∠3﹣∠1=2∠2 ④∠3>∠1+∠2.
正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进营业额不断增长,某大型超市决定购进甲、乙两种商品,已知甲种商品每件进价为150元,售价为168元;乙种商品每件进价为120元,售价为140元,该超市用42000元购进甲、乙两种商品,销售完后共获利5600元.
(1)该超市购进甲、乙两种商品各多少件?
(2)超市第二次以原价购进甲、乙两种商品共400件,且购进甲种商品的件数多于乙种商品的件数,要使第二次经营活动的获利不少于7580元,共有几种进货方案?写出利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
A.10
B.14
C.10或14
D.8或10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC与△DEF全等,A和D,B和F分别是对应顶点,下列结论正确的是( )
A. AB=DE B. ∠A=∠D C. ∠B=∠E D. AC=DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com