
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的曲边三角形的面积是 ;
围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.

【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OD,由AB是直径知∠ACB=90°,结合CD平分∠ACB知∠ABD=∠ACD=45°,从而知∠AOD=90°,根据曲边三角形的面积=S扇形AOD+S△BOD可得答案;
(2)由∠AOD=90°,即OD⊥AB,根据DE∥AB可得OD⊥DE,即可得证;
(3)勾股定理求得BC=8,作AF⊥DE知四边形AODF是正方形,即可得DF=5,由∠EAF=90°﹣∠CAB=∠ABC知tan∠EAF=tan∠CBA,即![]() ,求得EF的长即可得.
,求得EF的长即可得.
解:(1)如图,连接OD.∵AB是直径,且AB=10,
∴∠ACB=90°,AO=BO=DO=5.
∵CD平分∠ACB,∴∠ABD=∠ACD=![]() ∠ACB=45°,
∠ACB=45°,
∴∠AOD=90°,则曲边三角形的面积是
S扇形AOD+S△BOD=![]() +
+![]() ×5×5=
×5×5=![]() .
.
故答案为![]() ;
;
(2)由(1)知∠AOD=90°,即OD⊥AB.
∵DE∥AB,∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵AB=10、AC=6,∴BC=![]() =8.
=8.
过点A作AF⊥DE于点F,则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴![]() ,即
,即![]() ,
,
∴EF=![]() ,
,
∴DE=DF+EF=![]() +5=
+5=![]() .
.



 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】意外创伤随时可能发生,急救是否及时、妥善,直接关系到病人的安危.为普及急救科普知识,提高学生的急救意识与现场急救能力,某校开展了急救知识进校园培训活动.为了解七、八年级学生(七、八年级各有600名学生)的培训效果,该校举行了相关的急救知识竞赛.现从两个年级各随机抽取20名学生的急救知识竞赛成绩(百.分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,78,81,72,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 | |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 | c |
八年级 | 78 | d | 80.5 |
应用数据:
(1)由上表填空:a= ;b= ;c= ;d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在80分及以上的共有多少人?
(3)你认为哪个年级的学生对急救知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax.
(1)二次函数图象的对称轴是直线x= ;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
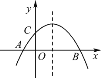
【题目】如图,已知抛物线![]() (m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(1)若抛物线过点(2,2),求抛物线的解析式;
(2)在(1)的条件下,抛物线的对称轴上是否存在一点H,使AH+CH的值最小,若存在,求出点H的坐标;若不存在,请说明理由;
(3)在第四象限内,抛物线上是否存在点M,使得以点A,B,M为顶点的三角形与△ACB相似?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
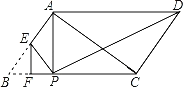
【题目】如图,AC是ABCD的对角线,∠BAC=90°,![]() ABC的边AB,AC,BC的长是三个连续偶数,E,F分别是边AB,BC上的动点,且EF⊥BC,将
ABC的边AB,AC,BC的长是三个连续偶数,E,F分别是边AB,BC上的动点,且EF⊥BC,将![]() BEF沿着EF折叠得到
BEF沿着EF折叠得到![]() PEF,连接AP,DP.若
PEF,连接AP,DP.若![]() APD为直角三角形时,BF的长为_____.
APD为直角三角形时,BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
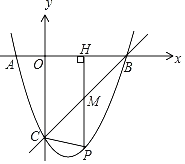
【题目】如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C.
(1)求抛物线的解析式;
(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?
查看答案和解析>>
科目:初中数学 来源: 题型:
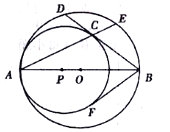
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 是半径
是半径![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为⊙
为⊙![]() 的半径,⊙
的半径,⊙![]() 的弦
的弦![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() .
.
(1)设![]() ,则
,则![]() 与
与![]() 之间的数量关系是什么?请说明理由.
之间的数量关系是什么?请说明理由.
(2)若![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,点
时,点![]() 是弦
是弦![]() 的中点.
的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com