
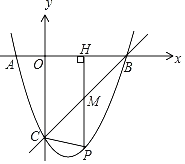
【题目】如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C.
(1)求抛物线的解析式;
(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)①有,![]() ;②存在,(2,﹣3)或(3﹣
;②存在,(2,﹣3)或(3﹣![]() ,2﹣4
,2﹣4![]() )
)
【解析】
(1)由直线表达式求出点B、C的坐标,将点B、C的坐标代入抛物线表达式,即可求解;
(2)①根据PM=(x﹣3)﹣(x2﹣2x﹣3)=﹣(x﹣![]() )2+
)2+![]() 即可求解;
即可求解;
②分PM=PC、PM=MC两种情况,分别求解即可.
解:(1)对于y=x﹣3,令x=0,y=﹣3,y=0,x=3,
故点B、C的坐标分别为(3,0)、(0,﹣3),
将点B、C的坐标代入抛物线表达式得:![]() ,
,
解得:![]() ,
,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)设:点M(x,x﹣3),则点P(x,x2﹣2x﹣3),
①有,理由:PM=(x﹣3)﹣(x2﹣2x﹣3)=﹣(x﹣![]() )2+
)2+![]() ,
,
∵﹣1<0,故PM有最大值,当x=![]() 时,PM最大值为:
时,PM最大值为:![]() ;
;
②存在,理由:
PM2=(x﹣3﹣x2+2x+3)2=(﹣x2+3x)2;
PC2=x2+(x2﹣2x﹣3+3)2;
MC2=(x﹣3+3)2+x2;
(Ⅰ)当PM=PC时,则(﹣x2+3x)2=x2+(x2﹣2x﹣3+3)2,
解得:x=0或2(舍去0),
故x=2,故点P(2,﹣3);
(Ⅱ)当PM=MC时,则(﹣x2+3x)2=(x﹣3+3)2+x2,
解得:x=0或3±![]() (舍去0和3+
(舍去0和3+![]() ),
),
故x=3﹣![]() ,则x2﹣2x﹣3=2﹣4
,则x2﹣2x﹣3=2﹣4![]() ,
,
故点P(3﹣![]() ,2﹣4
,2﹣4![]() ).
).
综上,点P的坐标为:(2,﹣3)或(3﹣![]() ,2﹣4
,2﹣4![]() ).
).


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】我们定义:在平面直角坐标系![]() 中,经过点
中,经过点![]() ,且平行于直线
,且平行于直线![]() 或
或![]() ,叫过该点的“二维线”.例如,点
,叫过该点的“二维线”.例如,点![]() 的“二维线”有:
的“二维线”有:![]() ,
,![]() .
.
(1)写出点![]() 的“二维线”______;
的“二维线”______;
(2)若点![]() 的“二维线”是
的“二维线”是![]() ,
,![]() ,求
,求![]() 、
、![]() 的值;
的值;
(3)若反比例函数![]() 图像上的一个点
图像上的一个点![]() 有一条“二维线”是
有一条“二维线”是![]() ,求
,求![]() 点
点![]() 的另一条“二维线”.
的另一条“二维线”.
查看答案和解析>>
科目:初中数学 来源: 题型:
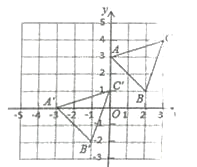
【题目】如图,三角形A’B’C是由三角形ABC经过某种平移得到的,点A与点A’,点B与点B’,点C与点C’分别对应,观察点与点坐标之间的关系,解答下列问题.
(1)分别写出点A、点B、点C、点A’、点B’、点C’的坐标,并说明三角形A’B’C’是由三角ABC经过怎样的平移得到的.
(2)若点M (a+2, 4-b)是点N (2a-3, 2b- 5)通过(1)中的变换得到的,求a和b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的曲边三角形的面积是 ;
围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月1日是新中国成立70周年.某学校国庆节后,为了调查学生对这场阅兵仪式的关注情况,在全校组织了一次全体学生都参加的“阅兵仪式有关知识”的考试,批改试卷后,学校政教处随机抽取了部分学生的考卷进行成绩统计,发现成绩最低是51分,最高是100分,根据统计结果,绘制了如下尚不完整的统计图表.
调查结果频数分布表
分数段/分 | 频数 | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
| 0.25 |
| 35 |
|
| 12 | 0.12 |
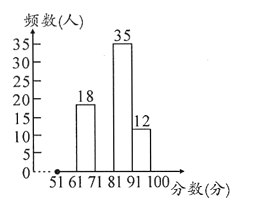
请根据以上信息,解答下列问题:
(1)![]() ;
;
(2)若把上面频数分布表中的信息画在扇形统计图内,则![]() 所在扇形圆心角的度数是 ;
所在扇形圆心角的度数是 ;
(3)请将频数分布直方图补充完整;
(4)若该校有1200名学生,请估计该校分数![]() 在
在![]() 范围的学生有多少名.
范围的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图8是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cm![]() a
a![]() b
b![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() h
h![]() 20cm,且 p
20cm,且 p![]() q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣活动课上,小致将等腰![]() 的底边
的底边![]() 与直线
与直线![]() 重合.
重合.
(1)如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 所在的直线
所在的直线![]() 上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小致发现
上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小致发现![]() 的最小值是____________.
的最小值是____________.
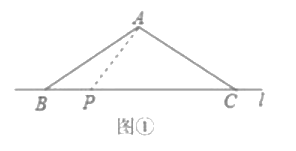
(2)为进一步运用该结论,在(1)的条件下,小致发现,当![]() 最短时,如图
最短时,如图![]() ,在
,在![]() 中,作
中,作![]() 平分
平分![]() 交
交![]() 于点
于点![]() 点
点![]() 分别是边
分别是边![]() 上的动点,连结
上的动点,连结![]() 小致尝试探索
小致尝试探索![]() 的最小值,小致在
的最小值,小致在![]() 上截取
上截取![]() 使得
使得![]() 连结
连结![]() 易证
易证![]() ,从而将
,从而将![]() 转化为
转化为![]() 转化到(1)的情况,则
转化到(1)的情况,则![]() 的最小值为 ;
的最小值为 ;
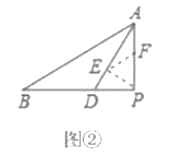
(3)解决问题:如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点,连结
上的动点,连结![]() 将线段
将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() 连结
连结![]() ,求线段
,求线段![]() 的最小值.
的最小值.
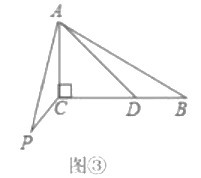
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com