
����Ŀ��ͬѧ����ȥ����ɽ���ڻ�ɽ����ɽ·�ϣ���һЩ�϶�������̨�ף���ͼ8�����еļס��Ҷ�̨��·��ʾ��ͼ��ͼ8�е����ֱ�ʾÿһ��̨�ĸ߶�(��λ:cm)��������d,e,e,c,c,d�ķ���p,����b,d,g,f,a,h�ķ���q��(10cm![]() a
a![]() b
b![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() h
h![]() 20cm,�� p
20cm,�� p![]() q������������ѧ�����й�ͳ��֪ʶ��ƽ��������λ��������ͼ���ش��������⣺
q������������ѧ�����й�ͳ��֪ʶ��ƽ��������λ��������ͼ���ش��������⣺
��1������̨��·����Щ��ͬ��Ͳ�ͬ�㣿
��2���Ķ�̨��·�������������Ϊʲô��
��3��Ϊ�����ο����ߣ���Ҫ����������ɽ��С·������������̨��·����̨�������������£�������������������飮

���𰸡���1������������2����̨�ף���3��������
��������
��1��������֪������ʾ��ͼ����ȷ����ͬ��Ͳ�ͬ�㣻
��2�����÷���Ķ��弴�ɽ�����⣻
��3������Ҫ�����ο����ߣ�Ҫ����������ɽ��С·������������̨��·����̨�������������£����÷���Ķ��弴�ɽ�����⣮
��1������֪��d,e,e,c,c,d�ķ���p,����b,d,g,f,a,h�ķ���q��(10cm![]() a
a![]() b
b![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() h
h![]() 20cm,�� p
20cm,�� p![]() q�������ʾ��ͼ����֪����ͬ�㣺��̨������̨�ĸ��߶Ȳβ�룬��ͬ�㣺��̨���߶ȵļ������̨��С��
q�������ʾ��ͼ����֪����ͬ�㣺��̨������̨�ĸ��߶Ȳβ�룬��ͬ�㣺��̨���߶ȵļ������̨��С��
��2����̨�ף���Ϊ��̨���߶ȵķ������̨��С��
��3��ʹ̨�ĸ��߶ȵķ���ԽСԽ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ�������ε�ֱ�Ƕ���������ԭ�㣬��OAB=30�㣬����A�ڷ���������y=![]() ��x��0����ͼ���ϣ�����B�ķ�������������ʽΪ��������
��x��0����ͼ���ϣ�����B�ķ�������������ʽΪ��������

A. y=��![]() B. y=��
B. y=��![]() C. y=��
C. y=��![]() D. y=
D. y=![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
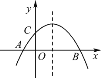
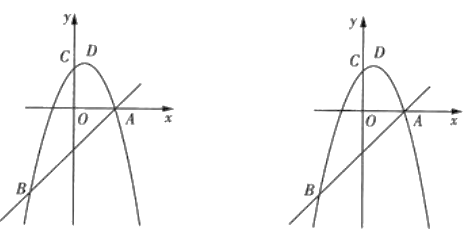
����Ŀ����ͼ����֪������![]() (m��0)��x���ཻ�ڵ�A��B����y���ཻ�ڵ�C���ҵ�A�ڵ�B�����.
(m��0)��x���ཻ�ڵ�A��B����y���ཻ�ڵ�C���ҵ�A�ڵ�B�����.
��1���������߹��㣨2��2�����������ߵĽ���ʽ��
��2���ڣ�1���������£������ߵĶԳ������Ƿ����һ��H��ʹAH+CH��ֵ��С�������ڣ������H�����ꣻ�������ڣ���˵�����ɣ�
��3���ڵ��������ڣ����������Ƿ���ڵ�M��ʹ���Ե�A��B��MΪ��������������ACB���ƣ������ڣ����m��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
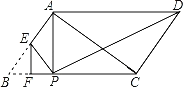
����Ŀ����ͼ��AC��ABCD�ĶԽ��ߣ���BAC��90����![]() ABC�ı�AB��AC��BC�ij�����������ż����E��F�ֱ��DZ�AB��BC�ϵĶ��㣬��EF��BC����
ABC�ı�AB��AC��BC�ij�����������ż����E��F�ֱ��DZ�AB��BC�ϵĶ��㣬��EF��BC����![]() BEF����EF�۵��õ�
BEF����EF�۵��õ�![]() PEF������AP��DP����
PEF������AP��DP����![]() APDΪֱ��������ʱ��BF�ij�Ϊ_____��
APDΪֱ��������ʱ��BF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
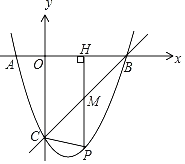
����Ŀ����ͼ����������y��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C��ֱ��y��x��3������B��C��
��1���������ߵĽ���ʽ��
��2����P��ֱ��BC�·���������һ���㣬����P��PH��x���ڵ�H����BC�ڵ�M������PC��
���߶�PM�Ƿ������ֵ������У�������ֵ�����û�У���˵�����ɣ�
���ڵ�P�˶��Ĺ����У��Ƿ���ڵ�M��ǡ��ʹ��PCM����PMΪ���ĵ��������Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ![]() ��ͼ
��ͼ![]() ����
����![]() ������������ÿ��С�����εĶ����Ϊ��㣬
������������ÿ��С�����εĶ����Ϊ��㣬![]() �Ķ�����ڸ���ϣ���
�Ķ�����ڸ���ϣ���![]() Ϊ��
Ϊ��![]() ���е㣮�ֱ���ͼ
���е㣮�ֱ���ͼ![]() ��ͼ
��ͼ![]() ��
��![]() �ı�
�ı�![]() ��ȷ����
��ȷ����![]() ������ֱ��
������ֱ��![]() ��ʹ
��ʹ![]() ��
��![]() ���ƣ�
���ƣ�
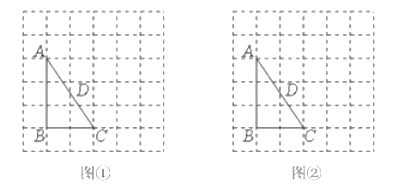
Ҫ��1��ͼ![]() ��ͼ
��ͼ![]() �еĵ�
�еĵ�![]() λ�ò�ͬ��
λ�ò�ͬ��
��2��ֻ���̶ȵ�ֱ�ߣ������ʵ�����ͼ�ۼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ������ؼ��Σ�����˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() �͵�
�͵�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1���������ߵĽ���ʽ������![]() �����ꣻ
�����ꣻ
��2��������ƽ�������ߣ�ʹ����![]() ����
����![]() ���ϣ�ԭ�����������ϵĵ�
���ϣ�ԭ�����������ϵĵ�![]() ƽ�ƺ�Ķ�Ӧ��Ϊ
ƽ�ƺ�Ķ�Ӧ��Ϊ![]() ����
����![]() �����
�����![]() �����ꣻ
�����ꣻ
��3�������������Ƿ���ڵ�![]() ʹ
ʹ![]() �������
�������![]() �����һ�룿�����ڣ�ֱ��д����
�����һ�룿�����ڣ�ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
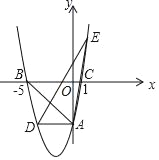
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx��5��y���ڵ�A����x���ڵ�B����5��0���͵�C��1��0��������A��AD��x�ύ�������ڵ�D��
��1����������ߵı���ʽ��
��2����E����������һ�㣬�ҵ�E����x��ĶԳƵ���ֱ��AD�ϣ����EAD�������
��3������P��ֱ��AB�·�����������һ���㣬����P�˶���ijһλ��ʱ����ABP�������������ʱ��P������͡�ABP����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com