
【题目】图![]() 、图
、图![]() 均是
均是![]() 的正方形网格,每个小正方形的顶点称为格点,
的正方形网格,每个小正方形的顶点称为格点,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 为边
为边![]() 的中点.分别在图
的中点.分别在图![]() 、图
、图![]() 中
中![]() 的边
的边![]() 上确定点
上确定点![]() 并作出直线
并作出直线![]() ,使
,使![]() 与
与![]() 相似.
相似.
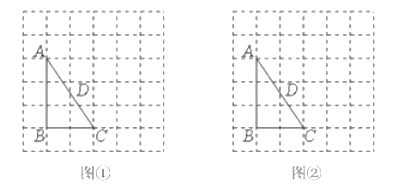
要求:(1)图![]() 、图
、图![]() 中的点
中的点![]() 位置不同.
位置不同.
(2)只用无刻度的直尺,保留适当的作图痕迹.
【答案】答案见解析
【解析】
(1)找到格点N、M,连接NM交AB于点P,过P点和D点作直线PD,P点即为所求,理由是:找到格点Q,连接NQ交AB于点T,连接TP,根据三角形相似的判定和性质,得到PT和AP的长,根据勾股定理和中点的性质,计算AD的长,再根据相似三角形的判定方法即可解决.
(2)找到格点K、L,连接KL与AB变动边的交点即为所求P点,理由为:根据三角形全等的判定和性质,证明P点为AB边的中点,然后根据中位线的意义和性质,结合三角形相似的判定方法,即可得出△APD∽△ABC;
解:(1)如图:找到格点N、M,连接NM交AB于点P,过P点和D点作直线PD,此时△APD∽△ACB.理由如下:
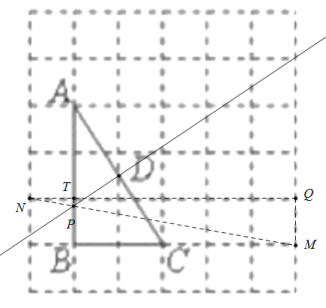
找到格点N、M、Q,连接NM交AB于点P,连接NQ交AB于点T,连接TP,由图可知,∠NTP=∠NQM,∠QNM=∠TNP,
∴△TNP∽△QNM,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
D为AC的中点,
∴![]() ,
,
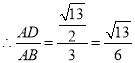 ,
,
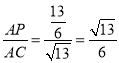 ,
,
在△APD和△ACB中,
∠DAP=∠BAC,
![]() ,
,
∴△APD∽△ACB.
(2)如图:找到格点K,L,连接KL,交AB于点P,过P点和D点作直线PD,此时△ABC∽△APD.理由如下:
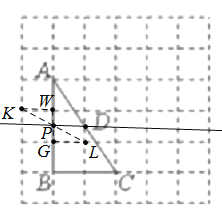
找到格点W、G,连接WG,KW,GL,由图可知,KW∥GL,
∴∠KPW=∠LPG,∠KWP=∠LGP,
又∵KW=LG,
∴△KWG≌LGP,
∴WP=GP,
∴P为WG的中点,
∵AW+WP=BG+GP,
∴AP=BP,
∴P为AB的中点,
∵D点为AC的中点,
∴PD为△ABC的中位线,
∴PD∥BC,
∴△APD∽△ABC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】速滑运动受到许多年轻人的喜爱,如图,梯形BCDG是某速滑场馆建造的速滑台,已知CD∥EG,高DG为4米,且坡面BC的坡度为1:1.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为1:![]() .
.
(1)求新坡面AC的坡角;
(2)原坡面底部BG的正前方10米(EB的长)处是护墙EF,为保证安全,体育管理部门规定,坡面底部至少距护墙7米.请问新的设计方案能否通过,试说明理由.(参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为
的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为![]() .
.
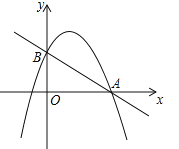
(1)求二次函数![]() 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足![]() 的自变量x的取值范围;
的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南灵宝苹果为中华苹果之翘楚,被誉为“中华名果”.某水果超市计划从灵宝购进“红富士”与“新红星”两种品种的苹果.已知2箱红富士苹果的进价与3箱新红星苹果的进价的和为282元,且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元.
(1)求每箱红富士苹果的进价与每箱新红星苹果的进价分别是多少元?
(2)如果购进红富士苹果有优惠,优惠方案是:购进红富士苹果超过20箱,超出部分可以享受七折优惠.若购进![]() (
(![]() ,且
,且![]() 为整数)箱红富士苹果需要花费
为整数)箱红富士苹果需要花费![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,超市决定在红富士、新红星两种苹果中选购其中一种,且数量超过20箱,请你帮助超市选择购进哪种苹果更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学:你去过黄山吗?在黄山的上山路上,有一些断断续续的台阶,如图8是其中的甲、乙段台阶路的示意图,图8中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q,(10cm![]() a
a![]() b
b![]() c
c![]() d
d![]() e
e![]() f
f![]() g
g![]() h
h![]() 20cm,且 p
20cm,且 p![]() q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
q),请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),与y轴的交点为C,已知﹣2≤c≤﹣1,顶点坐标为(1,n),则下列结论正确的是( )

A.a+b>0
B.![]()
C.对于任意实数m,不等式a+b>am2+bm恒成立
D.关于x的方程ax2+bx+c=n+1没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,E是边BC上一点,连接AE,过点D作DF⊥AE于点F.
(1)若AE=DA,求证:△ABE≌△DFA.
(2)若AB=6,AD=8,且E为BC中点.
①如图2,连接CF,求sin∠DCF的值.
②如图3,连接AC交DF于点M,求CM:AM的值.
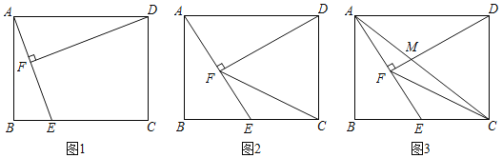
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变).
(1)写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.
(2)若货轮比游轮早36分钟到达衢州.问:
①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校鼓励师生利用课余时间广泛阅读,为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下单位:min)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
分段整理样本数据:
课外阅读时间 |
|
|
|
|
等级 | D | C | B | A |
人数 | 3 | ① | 8 | ② |
统计量:
平均数 | 中位数 | 众数 |
80 | ③ | ④ |
得出结论:
(1)填写表格中的数据:
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com