
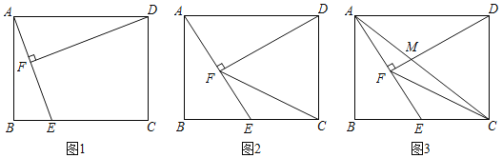
【题目】如图1,在矩形ABCD中,E是边BC上一点,连接AE,过点D作DF⊥AE于点F.
(1)若AE=DA,求证:△ABE≌△DFA.
(2)若AB=6,AD=8,且E为BC中点.
①如图2,连接CF,求sin∠DCF的值.
②如图3,连接AC交DF于点M,求CM:AM的值.
【答案】(1)见解析;(2)①![]() ,②
,②![]()
【解析】
(1)根据AAS证明三角形全等即可;
(2)①如图2中,过点F作FH⊥CD于H,FJ⊥AD于J.利用相似三角形的性质求出AF,DF,解直角三角形求出FJ,DJ,CH,FH即可解决问题;
②如图3中,延长DF交CB的延长线于K.利用相似三角形的性质求出KE,再利用平行线分线段成比例定理求解即可.
(1)证明:如图1中,
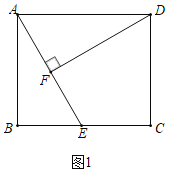
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠B=∠AFD=90°,
在△ABE和△DFA中
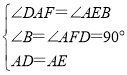 ,
,
∴△ABE≌△DFA(AAS).
(2)①解:如图2中,过点F作FH⊥CD于H,FJ⊥AD于J.
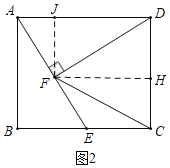
∵四边形ABCD是矩形,AB=CD=6,BC=AD=8,
∴∠B=90°,
∵BE=EC=4,
∴AE=![]() =
=![]() =2
=2![]() ,
,
∵∠DAF=∠AEB,∠B=∠AFD=90°,
∴△ABE∽△DFA,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴DF=![]() ,AF=
,AF=![]() ,
,
∵FJ⊥AD,
∴FJ=DH=![]() =
=![]() ,DJ=FH=
,DJ=FH=![]() =
=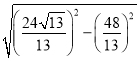 =
=![]() ,
,
∴CH=CD﹣DH=6﹣![]() =
=![]() ,
,
∴CF=![]() =
=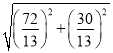 =6,
=6,
∴sin∠DCF=![]() =
=![]() =
=![]() .
.
②解:如图3中,延长DF交CB的延长线于K.
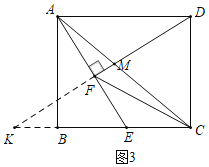
∵∠KEF=∠AEB,∠EFK=∠ABE=90°,
∴△KEF∽△AEB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴KE=5,
∴CK=KE+EC=9,
∵AD∥CK,
∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
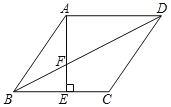
【题目】菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
①BF为∠ABE的角平分线;
②DF=2BF;
③2AB2=DFDB;
④sin∠BAE=![]() .其中正确的为( )
.其中正确的为( )
A.①③B.①②④C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
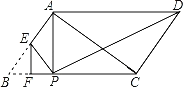
【题目】如图,AC是ABCD的对角线,∠BAC=90°,![]() ABC的边AB,AC,BC的长是三个连续偶数,E,F分别是边AB,BC上的动点,且EF⊥BC,将
ABC的边AB,AC,BC的长是三个连续偶数,E,F分别是边AB,BC上的动点,且EF⊥BC,将![]() BEF沿着EF折叠得到
BEF沿着EF折叠得到![]() PEF,连接AP,DP.若
PEF,连接AP,DP.若![]() APD为直角三角形时,BF的长为_____.
APD为直角三角形时,BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图![]() 、图
、图![]() 均是
均是![]() 的正方形网格,每个小正方形的顶点称为格点,
的正方形网格,每个小正方形的顶点称为格点,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 为边
为边![]() 的中点.分别在图
的中点.分别在图![]() 、图
、图![]() 中
中![]() 的边
的边![]() 上确定点
上确定点![]() 并作出直线
并作出直线![]() ,使
,使![]() 与
与![]() 相似.
相似.
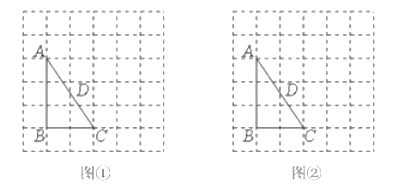
要求:(1)图![]() 、图
、图![]() 中的点
中的点![]() 位置不同.
位置不同.
(2)只用无刻度的直尺,保留适当的作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
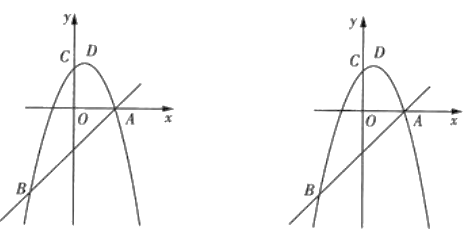
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)若向下平移抛物线,使顶点![]() 落在
落在![]() 轴上,原来的抛物线上的点
轴上,原来的抛物线上的点![]() 平移后的对应点为
平移后的对应点为![]() .若
.若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在抛物线上是否存在点![]() 使
使![]() 的面积是
的面积是![]() 面积的一半?若存在,直接写出点
面积的一半?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,交AB于点F,DF=BF,EA=EF.

(1)求证:△AEF为等边三角形;
(2)若CF⊥AB,①试说明DC = CF;②求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星星和阳阳是一对双胞胎,他们的爸爸买了两件不同图案的T恤给他们,星星和阳阳都想先挑选.于是阳阳设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的![]() 个小球,上面分别标有数字
个小球,上面分别标有数字![]() .一人先从袋中随机摸出一个小球,另一人再从袋中剩下的
.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的![]() 个小球中随机摸出一个小球.若摸出的两个小球上的数字之和为偶数,则星星先挑选;否则阳阳先挑选.
个小球中随机摸出一个小球.若摸出的两个小球上的数字之和为偶数,则星星先挑选;否则阳阳先挑选.
(1)用树状图或列表法求出星星先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com