
【题目】如图,平行四边形![]() 中,
中,![]() 和
和![]() 的平分线交于AD边上一点E,且
的平分线交于AD边上一点E,且![]() ,
,![]() ,则AB的长是( )
,则AB的长是( )
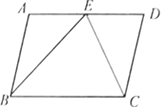
A. 2.5B. 3C. 4D. 2.4
【答案】A
【解析】
根据平行四边形的性质可证明△BEC是直角三角形,利用勾股定理可求出BC的长,利用角平分线的性质以及平行线的性质得出∠ABE=∠AEB,∠DEC=∠DCE,进而利用平行四边形对边相等进而得出答案.
∵四边形ABCD是平行四边形,∠ABC、∠BCD的角平分线的交点E落在AD边上,
∴∠ABE=∠EBC,∠DCE=∠ECB,AD//BC,AB//CD,
∴∠AEB=∠EBC,∠DEC=∠ECB,
∴∠ABE=∠AEB,∠DEC=∠DCE,
∴AB=AE,DE=DC,
∵AB//CD,
∴∠ABE+∠EBC+∠DCE+∠ECB=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
又∵BE=4,CE=3,
∴BC=![]() =5,
=5,
由题意可得:AB=CD,AD=BC,
∴AB=AE=![]() ,
,
故选A.


科目:初中数学 来源: 题型:
【题目】(1)如图①,ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
(2)如图②,将ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
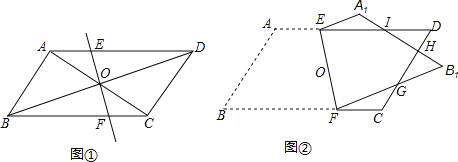
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一
A:计时制:0.05元/分,B:包月制:50元/月,此外,每一种上网时间都要收通信费0.02元/分
(1)某用户某月上网时间为x小时,请写出两种收费方式下该用户应该支付的费用(用y表示)
(2)若甲用户估计一个月上网时间为20小时,乙用户估计一个月上网时间为15小时,各选哪一种收费方式最合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
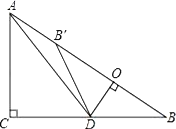
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球![]() 每个球除颜色外都相同
每个球除颜色外都相同![]() 的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验
的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验![]() 其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a=________,b=________,c=________;
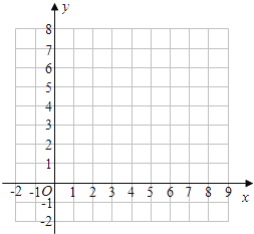
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.

(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com