
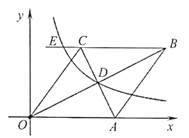
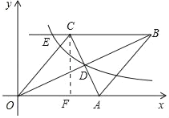
【题目】如图,在菱形![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,对角线
,对角线![]() 相交于点
相交于点![]() .双曲线
.双曲线![]() 经过点
经过点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,则过点
,则过点![]() 的双曲线表达式为()
的双曲线表达式为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过点C作CF⊥x轴于点F,由A点坐标可得菱形的边长,利用菱形面积可求出CF的长,由勾股定理可求出OF的长,即可得出C点坐标,进而可求出AC中点D的坐标,代入双曲线解析式可得k的值,根据CF的长可得E点纵坐标,代入双曲线解析式即可求出E点的横坐标,即可得答案.
过点C作CF⊥x轴于点F,
∵OBAC=160,A点的坐标为(10,0),
∴S菱形OABC=OACF=![]() OBAC=
OBAC=![]() ×160=80,菱形OABC的边长为10,
×160=80,菱形OABC的边长为10,
∴CF=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=![]() =
=![]() =6,
=6,
∴C(6,8),
∵点D是线段AC的中点,
∴D点坐标为(![]() ,
,![]() ),即(8,4),
),即(8,4),
∵双曲线y=![]() (x>0)经过D点,
(x>0)经过D点,
∴4=![]() ,即k=32,
,即k=32,
∴双曲线的解析式为:y=![]() (x>0),
(x>0),
故选:D.


科目:初中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的解析式及
的解析式及![]() 两点的坐标;
两点的坐标;
(2)求抛物线![]() 的顶点坐标;
的顶点坐标;
(3)将抛物线![]() 向上平移3个单位长度,再向右平移
向上平移3个单位长度,再向右平移![]() 个单位长度,得到抛物线
个单位长度,得到抛物线![]() .①若抛物线
.①若抛物线![]() 的顶点在
的顶点在![]() 内,求
内,求![]() 的取值范围;②若抛物线
的取值范围;②若抛物线![]() 与线段
与线段![]() 只有一个交点,直接写出
只有一个交点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
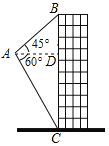
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为110m,那么该建筑物的高度BC约为_____m(结果保留整数,![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的![]() ,已知甲玩具的进货单价比乙玩具的进货单价多1元.
,已知甲玩具的进货单价比乙玩具的进货单价多1元.
(1)求:甲、乙玩具的进货单价各是多少元?
(2)玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
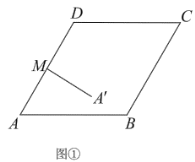
【题目】在边长为2的菱形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,若线段
边的中点,若线段![]() 绕点
绕点![]() 旋转得线段
旋转得线段![]() ,
,
(Ⅰ)如图①,线段![]() 的长__________.
的长__________.
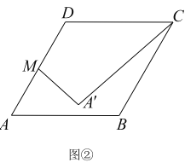
(Ⅱ)如图②,连接![]() ,则
,则![]() 长度的最小值是__________.
长度的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,![]() 辆大货车与
辆大货车与![]() 辆小火车一次可以运货
辆小火车一次可以运货![]() 吨,
吨,![]() 辆大货车与
辆大货车与![]() 辆小货车一次可以运货
辆小货车一次可以运货![]() 吨.
吨.
(1)求![]() 辆大货车和
辆大货车和![]() 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;
(2)现有![]() 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共![]() 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)在一个不透明的口袋装有三个完全相同的小球,分别标号为1、2、3.求下列事件的概率:
(1)从中任取一球,小球上的数字为偶数;
(2)从中任取一球,记下数字作为点A的横坐标x,把小球放回袋中,再从中任取一球记下数字作为点A的纵坐标y,点A(x,y)在函数![]() 的图象上.
的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的函数表达式是![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.若![]() ,函数的最大值是5
,函数的最大值是5
B.若![]() ,当
,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
C.无论a为何值时,函数图象一定经过点![]()
D.无论a为何值时,函数图象与x轴都有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形P和直线AB,给出如下定义:M为图形P上任意一点,N为直线AB上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P和直线AB之间的“确定距离”,记作d(P,直线AB).
已知A(2,0),B(0,2).
(1)求d(点O,直线AB);
(2)⊙T的圆心为![]() 半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
半径为1,若d(⊙T,直线AB)≤1,直接写出t的取值范围;
(3)记函数![]() 的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
的图象为图形Q.若d(Q,直线AB)=1,直接写出k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com