
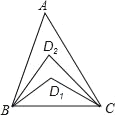
【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
【答案】25°
【解析】
根据题意可得∠ABC+∠ACB=160°,BD1,CD1,CD2,BD2…BDn,CDn是角平分线,可得∠ABDn+∠ACDn=160×(![]() )n,可求∠BCDn+∠CBDn的值,再根据三角形内角和定理可求结果.
)n,可求∠BCDn+∠CBDn的值,再根据三角形内角和定理可求结果.
∵∠A=20°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=160°,
∵BD1平分∠ABC,CD1平分∠ACB,
∴∠ABD1=![]() ABC,∠ACD1=
ABC,∠ACD1=![]() ∠ACD,
∠ACD,
∵BD2平分∠ABD1,CD2平分∠ACD1
∴∠ABD2=![]() ∠ABD1=
∠ABD1=![]() ∠ABC,∠ACD2=
∠ABC,∠ACD2=![]() ∠ACD1=
∠ACD1=![]() ∠ACB,
∠ACB,
同理可得∠ABD5=![]() ∠ABC,∠ACD5=
∠ABC,∠ACD5=![]() ∠ACB,
∠ACB,
∴∠ABD5+∠ACD5=160×![]() =5°,
=5°,
∴∠BCD5+∠CBD5=155°,
∴∠BD5C=180﹣∠BCD5﹣∠CBD5=25°
故答案为25°


科目:初中数学 来源: 题型:
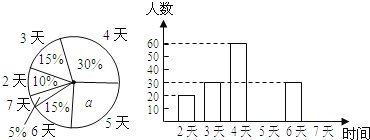
【题目】扬州市教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)参加调查的八年级学生总人数为_______人;
(2)根据图中信息,补全条形统计图;扇形统计图中“活动时间为4天”的扇形所对应的圆心角的度数为_______;
(3)如果全市共有八年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①(﹣2)101+(﹣2)100=﹣2100;②20172+2017一定可以被2018整除;③16.9×![]() +15.1×
+15.1×![]() 能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
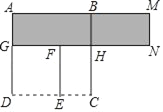
【题目】如图,四边形ABCD与四边形DEFG都是正方形,设AB=a,DE=b(a>b).
(1)写出AG的长度(用含字母a,b的代数式表示);
(2)观察图形,当用不同的方法表示图形中阴影部分的面积时,你能获得一个因式分解公式,请将这个公式写出来;
(3)如果正方形ABCD的边长比正方形DEFG的边长多16cm,它们的面积相差960cm2,试利用(2)中的公式,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
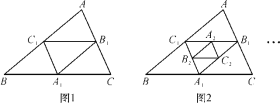
【题目】如图,在图1中,A1,B1,C1分别是△ABC的边BC,CA,AB的中点,在图2中,A2,B2,C2分别是△A1B1C1的边B1C1,C1A1,A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有___个.
查看答案和解析>>
科目:初中数学 来源: 题型:
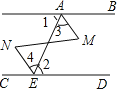
【题目】如图,直线AB,CD被直线AE所截,直线AM,EN被MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为已知条件,另一个作为结论,得出一个正确的命题.
(1)请按照:“∵ , ;∴ ”的形式,写出所有正确的命题;
(2)在(1)所写的命题中选择一个加以证明,写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,

若∠1:∠2:∠3=28:5:3,则∠α的度数是 ( )
A. 80° B. 100° C. 60° D. 45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com