
【题目】对任意一个三位数n,如果n满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
【答案】
(1)解:F(243)=(423+342+234)÷111=9; F(617)=(167+716+671)÷111=14
(2)解:∵s,t都是“相异数”,s=100x+32,t=150+y, ∴F(s)=(302+10x+230+x+100x+23)÷111=x+5,F(t)=(510+y+100y+51+105+10y)÷111=y+6.
∵F(t)+F(s)=18,
∴x+5+y+6=x+y+11=18,
∴x+y=7.
∵1≤x≤9,1≤y≤9,且x,y都是正整数,
∴ ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() .
.
∵s是“相异数”,
∴x≠2,x≠3.
∵t是“相异数”,
∴y≠1,y≠5.
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴  或
或 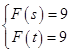 或
或  ,
,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴k的最大值为 ![]()
【解析】(1)根据F(n)的定义式,分别将n=243和n=617代入F(n)中,即可求出结论;(2)由s=100x+32、t=150+y结合F(s)+F(t)=18,即可得出关于x、y的二元一次方程,解之即可得出x、y的值,再根据“相异数”的定义结合F(n)的定义式,即可求出F(s)、F(t)的值,将其代入k= ![]() 中,找出最大值即可.
中,找出最大值即可.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )

A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D为AB上不与AB重合的一个动点,过点D分别作DE⊥AC于点E,DF⊥BC于点F,则线段EF的最小值为( )

A. 3 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
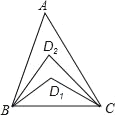
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-6x+a-2=0.
(1)如果该方程有实数根,求实数a的取值范围;
(2)如果该方程有两个相等的实数根,求出这两个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com