
【题目】已知抛物线y=-x2-mx+2m2(m<0)与x轴交于A,B两点,且点A在点B的左侧.
(1)求证:OB=2OA;
(2)若直线y=-x+2与抛物线只有一个公共点,求m的值.
(3)若点C与点O关于点A对称,且以点C为圆心,CO为半径的圆交抛物线于点D,求证:DO平分∠ADB.
【答案】(1)见解析;(2)当![]() 时,直线y=-x+2与抛物线只有一个公共点;(3)见解析.
时,直线y=-x+2与抛物线只有一个公共点;(3)见解析.
【解析】
(1)令y=0,代入y=-x2-mx+2m2,求出A(m,0),B(-2m,0),进而得OB=2OA;
(2)联立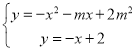 ,得x2+(m-1)x+(2-2m2)=0,结合直线y=-x+2与抛物线只有一个公共点,得△=0,进而即可求解;
,得x2+(m-1)x+(2-2m2)=0,结合直线y=-x+2与抛物线只有一个公共点,得△=0,进而即可求解;
(3)以点C为圆心,CO为半径的圆交抛物线于点D,交点有两个,分两种情况:①当D在x轴上方时,②当D在x轴下方时,分别求证,即可.
(1)∵抛物线y=-x2-mx+2m2(m<0)与x轴交于A、B两点,
∴关于x的方程-x2-mx+2m2=0有两个不相等的实数根x1和x2,
解得:x1=m,x2=-2m,
∵点A在点B的左边,且m<0,
∴A(m,0),B(-2m,0),
∴OA=-m,OB=-2m,
∴OB=2OA;
(2)∵直线y=-x+2与抛物线只有一个公共点,
∴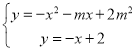 只有一组实数解,消y得:x2+(m-1)x+(2-2m2)=0,
只有一组实数解,消y得:x2+(m-1)x+(2-2m2)=0,
∴△=0,即(m-1)2-4×1×(2-2m2)=0,
整理得:9m2-2m-7=0,
解得:m1=1(不合题意舍去),![]() .
.
∴当![]() 时,直线y=-x+2与抛物线只有一个公共点;
时,直线y=-x+2与抛物线只有一个公共点;
(3)以点C为圆心,CO为半径的圆交抛物线于点D,交点有两个,
∴CO=CD,
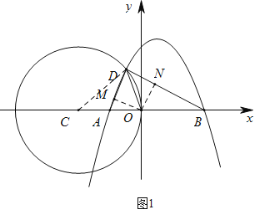
①当D在x轴上方时,如图1,连接CD,
∵点C与点O关于点A对称,
∴OC=2OA=2AC,
又由(1)得OB=2OA,
∴BC=2OC,
∴![]() =
=![]() ,
,
∵∠DCA=∠BCD,
∴△DCA∽△BCD,
∴BD=2AD,
∵OB=2OA,
∴S△BOD=2S△AOD,
过O点分别作△BOD、△AOD的高ON,OM,
∴S△BOD=![]() ,S△AOD=
,S△AOD=![]()
∴BDON=2ADOM,
∴ON=OM,
∴OD是∠ADB的平分线,即DO平分∠ADB;
②当D在x轴下方时,如图2,
同理①,可得DO平分∠ADB.
![]()


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
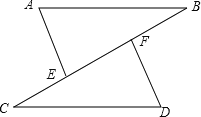
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:BE=CF.
(2)若AB=CF,∠B=40°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
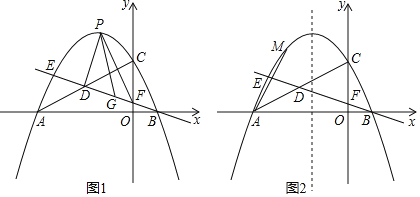
【题目】如图1,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)如图1,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() EG的值最小,求出PG﹣
EG的值最小,求出PG﹣![]() EG的最小值;
EG的最小值;
(2)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以点A、M、N、K为顶点的四边形是正方形时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
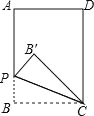
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
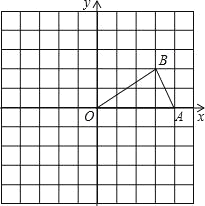
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD
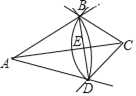
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,BC=2;
①求∠BAD所对的弧BD的长;②直接写出AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com