
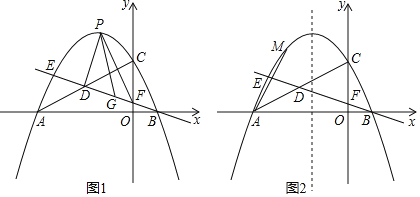
【题目】如图1,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)如图1,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() EG的值最小,求出PG﹣
EG的值最小,求出PG﹣![]() EG的最小值;
EG的最小值;
(2)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以点A、M、N、K为顶点的四边形是正方形时,直接写出点N的坐标.
【答案】(1)![]() ;(2)
;(2)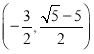 或
或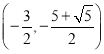 或
或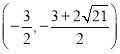 或
或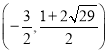 或
或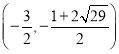 或
或![]() 或
或![]() .
.
【解析】
(1)△PDF的面积S=![]() ×PG×(xF﹣xD)=
×PG×(xF﹣xD)=![]() ×(
×(![]() +
+![]() x﹣
x﹣![]() )×2=﹣
)×2=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,当x=﹣
,当x=﹣![]() 时,S最大,即点P(﹣
时,S最大,即点P(﹣![]() ,
,![]() );GH=
);GH=![]() GE,故PG﹣
GE,故PG﹣![]() EG=PG﹣HG=PH为最小值,即点G为所求,即可求解;
EG=PG﹣HG=PH为最小值,即点G为所求,即可求解;
(2)分AM是正方形的边、对角线两种情况,每个情况分四个象限逐次求解即可.
解:(1)抛物线![]() ①,
①,
抛物线与x轴交于A,B两点,与y轴交于点C,
则点A、B、C的坐标为:(﹣4,0)、(1,0)、(0,2),则点D(﹣2,1),
函数的对称轴为x=﹣![]() ,
,
将点B、D的坐标代入一次函数表达式并解得:
直线BD的表达式为:y=﹣![]() x+
x+![]() ,
,
过点P作y轴的平行线交直线EF于点G,
设点P(x,![]() ),则点G(x,﹣
),则点G(x,﹣![]() x+
x+![]() ),
),
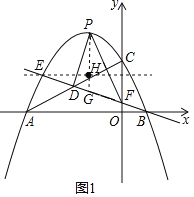
△PDF的面积S=![]() ×PG×(xF﹣xD)=
×PG×(xF﹣xD)=![]() ×(
×(![]() +
+![]() x﹣
x﹣![]() )×2=﹣
)×2=﹣![]() x2﹣
x2﹣![]() x+
x+![]()
当x=﹣![]() 时,S最大,即点P(﹣
时,S最大,即点P(﹣![]() ,
,![]() );
);
过点E作x轴的平行线交PG于点H,
直线BD的表达式为:y=﹣![]() x+
x+![]() ②,
②,
则tan∠EBA=![]() =tan∠HEG,
=tan∠HEG,
GH=![]() GE,故PG﹣
GE,故PG﹣![]() EG=PG﹣HG=PH为最小值,即点G为所求,
EG=PG﹣HG=PH为最小值,即点G为所求,
联立①②并解得:x=﹣![]() ,故点E(﹣
,故点E(﹣![]() ,
,![]() ),
),
则PG﹣![]() EG的最小值PH:
EG的最小值PH:![]() ﹣
﹣![]() =
=![]() ;
;
(2)①当AM是正方形的边时,
(Ⅰ)当点M在y轴左侧时(N在下方),如图2,
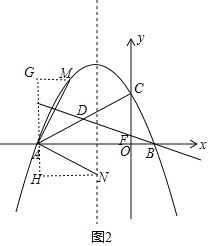
当点M在第二象限时,
过点A作y轴的平行线GH,过点M作MG⊥GH与点G,过点N作HN⊥GH于点H,
∵∠GMA+∠GAM=90°,∠GAM+∠HAN=90°,∴∠HAN=∠GMA,
∠AGM=∠NHA=90°,AM=AN,∴△AGM≌△NHA(AAS),
∴GA=NH=4﹣![]() =
=![]() ,AH=GM,
,AH=GM,
即![]() =
=![]() ,解得:x=
,解得:x=![]() ,
,
当x=![]() 时,则GM=x﹣(﹣4)=
时,则GM=x﹣(﹣4)=![]() ,
,
点yN=﹣AH=﹣GM=![]() ,
,
故点N(﹣![]() ,
,![]() );
);
当x=![]() 时,同理可得:点N(﹣
时,同理可得:点N(﹣![]() ,﹣
,﹣![]() );
);
当点M在第三象限时,
同理可得:点N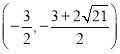 ;
;
(Ⅱ)当点M在y轴右侧时,
如图3,M在第一象限时,
过点M作MH⊥x轴于点H,
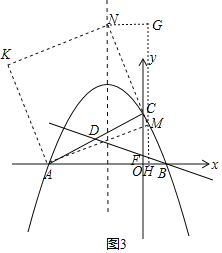
设AH=b,MH=a,
同理可得:△AHM≌△MGN(AAS),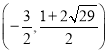
则点M(﹣4+b,b﹣![]() ),即a=b﹣
),即a=b﹣![]() ,
,
将点M的坐标代入①式并解得:b=![]() ,a=
,a=![]() (a、b均舍去负值),
(a、b均舍去负值),
yN=a+b=![]() ,
,
故点N(﹣![]() ,
,![]() ),
),
同理当点M在第四象限时,点N(﹣![]() ,-
,-![]() );
);
②当AM是正方形的对角线时,
当点M在y轴左侧时,
过点M作MG垂直于函数对称轴于点G,设函数对称轴与x轴交于点H,
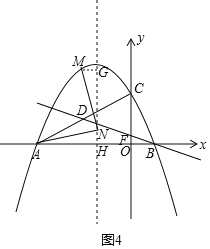
同理可得:△AHN≌△NGM(AAS),
设点N(﹣![]() ,m),则点M(﹣
,m),则点M(﹣![]() ﹣m,
﹣m,![]() +m),
+m),
将点M的坐标代入①式并解得:m=![]() 或﹣
或﹣![]() (舍去),
(舍去),
故点N(﹣![]() ,
,![]() );
);
当点M在y轴右侧时,
同理可得:点N(﹣![]() ,﹣
,﹣![]() ).
).
综上,点N的坐标为: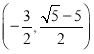 或
或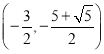 或
或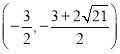 或
或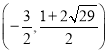 或
或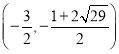 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】有一 列数是7、9、3、7、6、9、11、8、 2、9、10,中位数是多少?这列数若再加入3和1000两个数,那么中位数会改变吗?平均数又会有什么变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
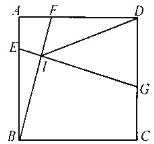
【题目】如图,在边长为6的正方形ABCD中,点E、F、G分别在边AB、AD、CD上,EG与BF交于点I,AE=2,BF=EG,DG>AE,则DI的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
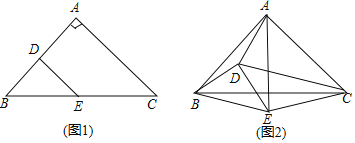
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2,点D、E分别是AB、BC的中点,把△BDE绕点B旋转,连接AD、AE、CD、CE,如图2.
(1)求证:△BDE∽△BAC.
(2)求△ABE面积最大时,△ADE的面积.
(3)在旋转过程中,当点D落在△ACE的边所在直线上时,直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校各有200名体训队队员,为了解这两校体训队员的体能,进行了抽样调查过程如下,请补充完整
收集数据:从甲、乙两个学校各随机抽取20名体课队员,讲行体能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据:按如下分数段整理、描述这两组样本数据:
成绩x人数 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲校 | 0 | 0 | 1 | 11 | 7 | 1 |
乙校 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体能优秀,70~79分为体能良好,60~69为体能合格,60以下为体能不合格)
分析数据:两组样本数据的平均数、中位数、众数如下表所示
学校 | 平均数 | 中位数 | 众数 | 优秀率 |
甲 | 78.3 | 77.5 | b | 40% |
乙 | 78 | a | 81 | c |
问题解决:(1)直接写出a,b,c的值;
(2)估计甲校90分及以上的学生有多少人.
(3)得出结论:通过以上数据的分析,你认为哪个学校的体训队学生的体能水平更高,并从两个不同的角度说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,![]() 的最小值为0;
的最小值为0;![]() .当
.当![]() 时有
时有![]() ;且对于任意实数
;且对于任意实数![]() ,
,![]() .
.
(1)![]() 的对称轴为_________,顶点坐标为_____________;
的对称轴为_________,顶点坐标为_____________;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)令![]() ,试求实数
,试求实数![]() ,使得实数
,使得实数![]() 最大,当
最大,当![]() 时
时![]() 成立.
成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2-mx+2m2(m<0)与x轴交于A,B两点,且点A在点B的左侧.
(1)求证:OB=2OA;
(2)若直线y=-x+2与抛物线只有一个公共点,求m的值.
(3)若点C与点O关于点A对称,且以点C为圆心,CO为半径的圆交抛物线于点D,求证:DO平分∠ADB.
查看答案和解析>>
科目:初中数学 来源: 题型:
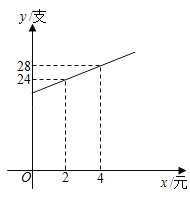
【题目】小李经营的车饰店销售某品牌车漆修复液,已知其进价为40元/支,试销阶段发现将售价定为80元/支时,每天可销售20支,后来为了扩大销售量,小李适当降低了售价,销售量y(支)与降价x(元)的关系如图所示.
(1)请仔细读题,并补全下面表格:
降价x/元 | … | 2 | 4 |
| x | … |
销量y/支 | … | 24 | 28 | 30 |
| … |
(2)若要使得平均每天销售这种修复液的利润W最大,则每支修复液应该降价多少元?最大的利润W为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为第一象限内的一点,当
为第一象限内的一点,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,连接
为斜边的等腰直角三角形时,连接![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并写出自变量
,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置(
的位置(![]() 与
与![]() 对应),若
对应),若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com