
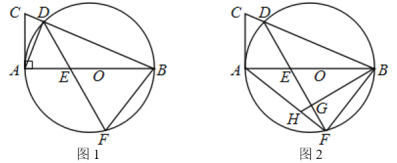
【题目】如图1,AB为⊙O的直径,AC与⊙O相切于点A,BC与⊙O交于点D,点F是直径AB下方半圆上一点(不与A,B重合),连接DF,交AB于点E,
(1)求证:∠C=∠F;
(2)如图2,若DF=DB,连接AF.
①求证:∠FAE=2∠AFE;
②作BH⊥FD于点G,与AF交于点H.若AH=2HF,CD=1,求BG的长.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)利用等角的余角相等以及圆周角定理即可解决问题.
(2)①如图2中,连接DO,延长DO交BF于K.想办法证明AF∥DK,利用等腰三角形的性质证明∠FDB=2∠AFD即可解决问题.
②如图2中,设DK交BH于J,连接JF.首先证明四边形AFJD是平行四边形,推出![]() ,设GH=m,GJ=3m,则JH=JF=JB=4m,推出GF=
,设GH=m,GJ=3m,则JH=JF=JB=4m,推出GF=![]() =
=![]() m,由∠C=∠BFG,推出tanC=tan∠BFG=
m,由∠C=∠BFG,推出tanC=tan∠BFG=![]() =
=![]() =
=![]() ,求出AD即可解决问题.
,求出AD即可解决问题.
解:(1)证明:如图1中,
∵AC是切线,
∴AB⊥AC,
∴∠CAB=90°,
∵AB是直径,
∴∠ADB=∠ADC=90°,
∵∠C+∠CAD=90°,∠CAD+∠DAB=90°,
∴∠C=∠DAB,
∵∠DAB=∠F,
∴∠C=∠F.

(2)①证明:如图2中,连接DO,延长DO交BF于K.
∵DF=DB,
∴![]() ,
,
∴DK⊥BF,
∴∠FDK=∠BDK,
∵AB是直径,
∴∠AFB=∠DKB=90°,
∴DK∥AF,
∴∠AFD=∠FDK,
∴∠FDB=2∠AFD,
∵∠EAF=∠FDB,
∴∠EAF=2∠BDF.
②解:如图2中,设DK交BH于J,连接JF.
∵DF=DB,DK⊥FB,
∴FK=BK,
∴JF=JB,
∴∠JFB=∠JBF,
∵∠JFB+∠JFH=90°,∠JBF+∠BHF=90°,
∴∠JFH=∠JHF,
∵DK⊥BF,BG⊥DF,
∴FJ⊥DB,
∵AD⊥BD,
∴AD∥FJ,
∵AF∥DJ,
∴四边形AFJD是平行四边形,
∵AH=2FH,
∴可以假设HF=a,AH=2a,
∴DJ=AF=3a,
∵FH∥DJ,
∴![]() ,设GH=m,GJ=3m,则JH=JF=JB=4m,
,设GH=m,GJ=3m,则JH=JF=JB=4m,
∴GF=![]() =
=![]() m,
m,
∵∠C=∠BFG,
∴tanC=tan∠BFG=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵CD=1,
∴AD=FJ=BJ=![]() ,
,
∴4m=![]()
∴m=![]() ,
,
∴BG=7m=![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
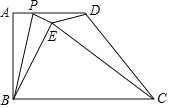
【题目】如图,四边形ABCD中,AD∥BC,AB⊥BC,点P是边AD上一动点,将△ABP沿BP折叠得到△BEP,连接DE,CE,已知AB=4,AD=3,BC=6,则△CDE面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
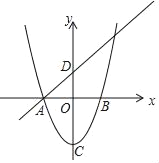
【题目】如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求线段AD的长;
(2)平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
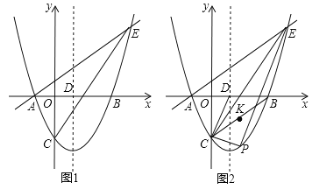
(1)求直线![]() 的解析式.
的解析式.
(2)点![]() 为直线
为直线![]() 下方抛物线上的一点,连接
下方抛物线上的一点,连接![]() ,
,![]() .当
.当![]() 的面积最大时,连接
的面积最大时,连接![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一点,点
上的一点,点![]() 是线段
是线段![]() 上的一点,求
上的一点,求![]() 的最小值.
的最小值.
(3)点![]() 是线段
是线段![]() 的中点,将抛物线
的中点,将抛物线![]() 与
与![]() 轴正方向平移得到新抛物线
轴正方向平移得到新抛物线![]() ,
,![]() 经过点
经过点![]() ,
,![]() 的顶点为点
的顶点为点![]() ,在新抛物线
,在新抛物线![]() 的对称轴上,是否存在点
的对称轴上,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机抽取某小吃店一周的营业额(单位: 元)如下表:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
|
|
|
|
|
|
|
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月(按![]() 天计算)的营业额,星期一到星期五营业额相差不大,用这
天计算)的营业额,星期一到星期五营业额相差不大,用这![]() 天的平均数估算合适么?简要说明理由.
天的平均数估算合适么?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
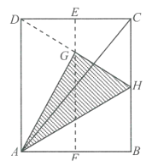
【题目】如图,在一张矩形纸片![]() 中,对角线
中,对角线![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点,现将这张纸片折叠,使点
的中点,现将这张纸片折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() 的延长线恰好经过点
的延长线恰好经过点![]() ,则点
,则点![]() 到对角线
到对角线![]() 的距离为( )
的距离为( )![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学参加“创文明城市”书画比赛时,老师从全校![]() 个班中随机抽取了
个班中随机抽取了![]() 个班(用
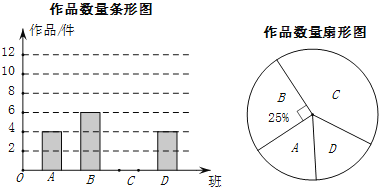
个班(用![]() 表示),对抽取的作品的数量进行了分析统计,制作了两幅不完整的统计图.回答下列问题:
表示),对抽取的作品的数量进行了分析统计,制作了两幅不完整的统计图.回答下列问题:
(1)老师采用的调查方式是 .(填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中![]() 班作品数量所对应的圆心角度数 度.
班作品数量所对应的圆心角度数 度.
(3)请估计全校共征集作品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
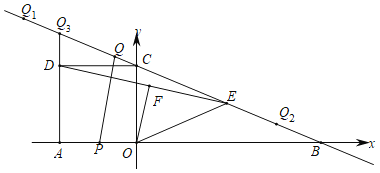
(1)求点B的坐标和OE的长;
(2)设点Q2为(m,n),当![]() tan∠EOF时,求点Q2的坐标;
tan∠EOF时,求点Q2的坐标;
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com