Question

14．如图，在平面直角坐标系中．矩形ABCD的顶点A与坐标原点O重合．点B和点D分别在x轴与y轴的正半轴上．双曲线y=$\frac{k}{x}$（x＞0）经过顶点C，直线y=-x+2经过顶点B交y轴与点E，（点E在点D的上方），点D关于直线y=-x+2的对称点F也在双曲线y=$\frac{k}{x}$上．
（1）∠BE0=45°；
（2）求实数k的值；
（3）将矩形ABCD进行适当的平移，设平移后矩形的顶点B的坐标为（m，n）
①若点B，D均在双曲线y=$\frac{k}{x}$上（如图2），求m的值；
②若双曲线y=$\frac{k}{x}$分别交边BC、CD与点M，N（如图3），判断是否存在合适的平移使MN∥BD？若存在，求此时m与n应满足的关系式；若不存在，说明理由．

Answer 1

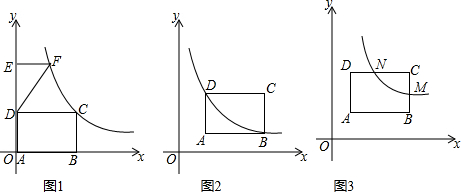
分析 （1）由B，E是直线y=-x+2与x轴，y轴的交点，于是得到E（0，2），B（2，0），求得OE=OB=2，即可得到结论；
（2）在矩形ABCD中，AB=CD，AD=BC，由E（0，2），B（2，0），得到D（0，b），DE=EF=2-b，推出△DEG是等腰直角三角形，由于点D关于直线y=-x+2的对称点F，连接FG，则四边形DEFG是正方形，得到F点坐标为（2-b，2），代入y=$\frac{2b}{x}$中得b=1，求得k=2b=2；
（3）①由题意，点D的坐标为（m-2，n+1），将B，D两点坐标代入反比例函数解析式中得方程组即可得到结果；
②存在．由题意得到M（m，$\frac{2}{m}$），N（$\frac{2}{n+1}$，n+1），C（m，n+1），由于MN∥BD，于是得到$\frac{CM}{CB}$=$\frac{CN}{CD}$=2，求得CN=m-$\frac{2}{n+1}$=$\frac{mn+m-2}{n+1}$≠0，CM=n+1-$\frac{2}{m}$=$\frac{mn+m-2}{m}$≠0，由于mn+m-2≠0，CN=2CM，于是得到$\frac{mn+m-2}{n+1}=2×\frac{mn+m-2}{m}$，化简得到$\frac{1}{n+1}=\frac{2}{m}$，于是求得结论．

解答 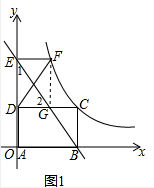解：（1）∵B，E是直线y=-x+2与x轴，y轴的交点，
∴E（0，2），B（2，0），
∴OE=OB=2，
∵∠BOE=90°，
∴∠BEO=45°，
故答案为：45°；

（2）在矩形ABCD中，AB=CD，AD=BC，
∵E（0，2），B（2，0），
∴OE=OB=2，
∴D（0，b），DE=EF=2-b，
∵∠1=∠2=45°，
∴△DEG是等腰直角三角形，∵
点D关于直线y=-x+2的对称点F，
连接FG，则四边形DEFG是正方形，
∴F点坐标为（2-b，2），代入y=$\frac{2b}{x}$中得b=1，
∴k=2b=2；

（3）①由题意，点D的坐标为（m-2，n+1），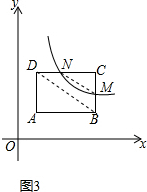
将B，D两点坐标代入反比例函数解析式中得$\left\{\begin{array}{l}{mn=2}\\{（m-2）（n+1）=2}\end{array}\right.$，
解得m=1+$\sqrt{5}$或m=1-$\sqrt{5}$（舍去）；
②存在．
由题意，M（m，$\frac{2}{m}$），N（$\frac{2}{n+1}$，n+1），C（m，n+1），
∵MN∥BD，
∴$\frac{CM}{CB}$=$\frac{CN}{CD}$=2，
∵B（m，n），BC=1，
∴CN=m-$\frac{2}{n+1}$=$\frac{mn+m-2}{n+1}$≠0，CM=n+1-$\frac{2}{m}$=$\frac{mn+m-2}{m}$≠0，
∴mn+m-2≠0，∵CN=2CM，
∴$\frac{mn+m-2}{n+1}=2×\frac{mn+m-2}{m}$，
∴$\frac{1}{n+1}=\frac{2}{m}$，
∴m=2（n+1），
∴MN∥BD时，m与n应满足的关系式是m=2（n+1）．

点评 本题考查了由函数解析式求点的坐标，等腰直角三角形的性质，矩形的性质，联立方程组求得字母的值，平行线分线段成比例定理，轴对称的性质，熟练掌握各知识点是解题的关键．