
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.


【拓展延伸】
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
【答案】∠P=![]() α+
α+![]() β.
β.
【解析】试题分析:(1)根据三角形内角和定理即可证明.
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
(3)表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
(4)列出方程组即可解决问题.
试题解析:(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D;
(2) 如图2,∵AP、CP分别平分∠BAD、∠BCD,
∴∠1=∠2,∠3=∠4,
∵∠2+∠B=∠3+∠P,
∠1+∠P=∠4+∠D,
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°;
×(36°+16°)=26°;
(3)如图3,
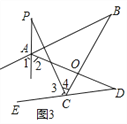
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,∴∠PAD=180°-∠2,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠D+(180°-∠3),∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°;
×(36°+16°)=26°;
(4)∠P=![]() α+
α+![]() β.
β.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′ 、C′ ;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为 ;
运用与拓广:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() +bx﹣
+bx﹣![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)b= ;点D的坐标: ;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
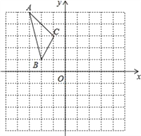
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
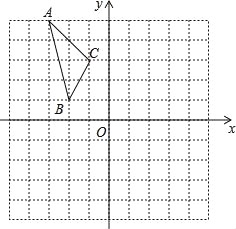
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到![]() ,已知点
,已知点![]() 的坐标为(4,0),写出顶点
的坐标为(4,0),写出顶点![]() ,
,![]() 的坐标;
的坐标;
(2)若△ABC和![]() 关于原点O成中心对称图形,写出
关于原点O成中心对称图形,写出![]() 的各顶点的坐标;
的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到![]() ,写出
,写出![]() 的各顶点的坐标.
的各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com