
【题目】如图,二次函数y=![]() +bx﹣
+bx﹣![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)b= ;点D的坐标: ;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.

【答案】(1)1;(﹣3,4);(2)线段AO上不存在点P(点P不与A、O重合),使得OE的长为1 ;(3)![]() .
.
【解析】
试题分析:(1)利用点在二次函数图象上,代入即可求得b,将二次函数换成交点式,即能得出B点的坐标,由AD=AB可算出D点坐标;
(2)假设存在,由DP⊥AE,找出∠EPO=∠PDA,利用等角的正切相等,可得出一个关于OP长度的一元二次方程,由方程无解可得知不存在这样的点;
(3)利用角和边的关系,找到全等,再利用三角形相似,借助相似比即可求得AM,求出△ADM的面积即是所求.
试题解析:(1)∵点A(﹣3,0)在二次函数y=![]() +bx﹣
+bx﹣![]() 的图象上,
的图象上,
∴0=![]() ﹣3b﹣
﹣3b﹣![]() ,解得b=1,
,解得b=1,
∴二次函数解析式为y=![]() +x﹣
+x﹣![]() =
=![]() (x+3)(x﹣1),
(x+3)(x﹣1),
∴点B(1,0),AB=1﹣(﹣3)=4,
∵四边形ABCD为正方形,
∴AD=AB=4,
∴点D(﹣3,4),
故答案为:1;(﹣3,4).
(2)直线PE交y轴于点E,如图1,

假设存在点P,使得OE的长为1,设OP=a,则AP=3﹣a,
∵DP⊥AE,∠APD+∠DPE+∠EPO=180°,
∴∠EPO=90°﹣∠APD=∠ADP,
tan∠ADP=![]() =
=![]() ,tan∠EPO=
,tan∠EPO=![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() ﹣3a+4=0,
﹣3a+4=0,
△=![]() ﹣4×4=﹣7<0,无解,
﹣4×4=﹣7<0,无解,
故线段AO上不存在点P(点P不与A、O重合),使得OE的长为1.
(3)假设存在这样的点P,DE交x轴于点M,如图2,
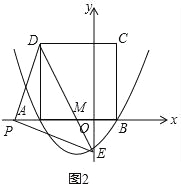
∵△PED是等腰三角形,
∴DP=PE,
∵DP⊥PE,四边形ABCD为正方形
∴∠EPO+∠APD=90°,∠DAP=90°,∠PAD+∠APD=90°,
∴∠EPO=∠PDA,∠PEO=∠DPA,
在△PEO和△DAP中,
∠EPO=∠PDA,DP=PE,∠PEO=∠DPA,
∴△PEO≌△DAP,
∴PO=DA=4,OE=AP=PO﹣AO=4﹣3=1,
∴点P坐标为(﹣4,0).
∵DA⊥x轴,
∴DA∥EO,
∴∠ADM=∠OEM(两直线平行,内错角相等),
又∵∠AMD=∠OME(对顶角),
∴△DAM∽EOM,
∴![]() ,
,
∵OM+MA=OA=3,
∴MA=![]() ×3=
×3=![]() ,
,
△PED与正方形ABCD重叠部分△ADM面积为![]() ×AD×AM=
×AD×AM=![]() ×4×
×4×![]() =
=![]() .
.
答:存在这样的点P,点P的坐标为(﹣4,1),此时△PED与正方形ABCD重叠部分的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.


【拓展延伸】
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对抛物线y=-2(x-1)2+3性质的描写中,正确的是( )
A.开口向上B.对称轴是直线x=1C.顶点坐标是(-1,3)D.函数y有最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D.
(1)求证:∠BAD=∠CBD;
(2)求证:DE=DB.
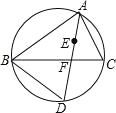
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com