
 如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60°得到BN,连接BN、AM、CM.
如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60°得到BN,连接BN、AM、CM.| 2 |
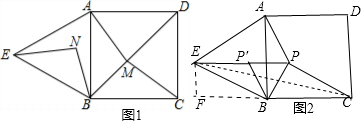 解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,
解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,
|
 ∴△AMB≌△ENB(SAS),
∴△AMB≌△ENB(SAS),
| ||
| 2 |
| 2 |
| ||
| 2 |
2
| ||||
| 2 |
| AM |
| cos15° |
| 3 |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源:2014-2015学年内蒙古化德县第三中学九年级上学期期末测试数学试卷(解析版) 题型:选择题
如图所示,随机闭合开关K1,K2,K3中的两个,则能让两盏灯泡同时发光的概率为( )
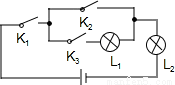
A.1 B.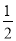 C.
C.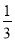 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
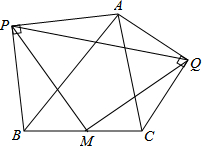 如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.
如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com