
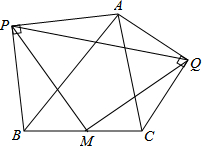
 如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.
如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形. 证明:作AB的中点D,AC的中点E 连MD,ME PD,QE,
证明:作AB的中点D,AC的中点E 连MD,ME PD,QE,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
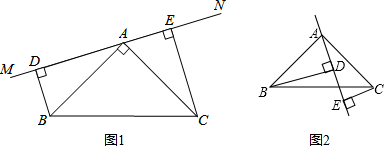
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60°得到BN,连接BN、AM、CM.
如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60°得到BN,连接BN、AM、CM.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,是一个转盘,转盘被分成两个扇形,颜色分为白黑黄两种,黑色扇形的圆心角为150°,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)则指针指向黑色扇形的概率是
如图,是一个转盘,转盘被分成两个扇形,颜色分为白黑黄两种,黑色扇形的圆心角为150°,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)则指针指向黑色扇形的概率是查看答案和解析>>
科目:初中数学 来源: 题型:
| A、122,32 |
| B、120,32 |
| C、124,30 |
| D、110,32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com