
(12分)如图①,OP是∠MON的平分线。
(1)请你利用该图形画一对以OP所在直线为对称轴的全等三角形。(3分)请你参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60゜,AD、CE分别是∠BAC,∠BCA的平分线,AD、CE相交于点F,请你判断并写出EF与DF之间的数量关系并证明。(7分)
(3)如图③,在△ABC中,如果∠ACB不是直角,而(2)中的其他条件不变。请问,你在(2)中所得结论是否仍然成立? ______________ (填 是或否)。(2分)
(2)证明:

见解析
【解析】
试题分析:(1)提到角平分线就会想到角平分线上的点到角两边的距离相等,就要做辅助线(过角平分线上的任一点到角两边的距离),构造全等三角形
(2)过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,从而根据角平分线的性质得证△DMF≌△ENF,最终得出结果;
(3)过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,从而根据角平分线的性质得证△DMF≌△ENF,因此可判断.
试题解析:(1)

(2)②相等,过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,

∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∵在Rt△ABC中,∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∴
∴∠CDA=75°,
∵∠MFC=45°,∠MFN=120°,
∴∠NFE=15°,
∴∠NEF=75°=∠MDF,
∴△DMF≌△ENF,
∴FE=FD;
③是.
过点F作FM⊥BC于M.作FN⊥AB于N,连接BF,
∵F是角平分线交点,
∴BF也是角平分线,
∴MF=FN,∠DMF=∠ENF=90°,
∴四边形BNFM是圆内接四边形,
∵∠B=60°,
∴∠MFN=180°-∠B=120°,
∵
∴∠DFE=∠CFA=120°.
又∵∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,
∴∠DFM=∠DFE,
∴△DMF≌△ENF,
∴FE=FD.
考点:角平分线的性质,三角形全等的判定与性质


科目:初中数学 来源:浙教版(2014) 七年级上 题型:
| |||||
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省绍兴市六校九年级上学期第一次联考数学试卷(解析版) 题型:填空题
正比例函数 与反比例函数
与反比例函数 在同一平面直角坐标系中的图象如图所示,则当
在同一平面直角坐标系中的图象如图所示,则当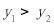 时
时 的取值范围是_________.
的取值范围是_________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校九年级上学期期中测试数学试卷(解析版) 题型:选择题
如图,AB和CD都是⊙O的直径,∠AOC=52°,则∠C的度数是( )

A.22° B.26° C.38° D.48°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=___________度.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中考试数学试卷(解析版) 题型:解答题
(6分)请分别画出下图中各图的所有对称轴.
(1)正方形 (2)正三角形 (3)相交的两个圆

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市塘下学区七年级上学期期中联考数学试卷(解析版) 题型:解答题
(本小题6分)如图所示的3×3的方格中,用 画出3个面积
画出3个面积 9的不同的正方形,而且所画正方形的顶点都在方格的顶点上,并写出你所画的正方形的边长.
9的不同的正方形,而且所画正方形的顶点都在方格的顶点上,并写出你所画的正方形的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com