
����Ŀ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() ���
���![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬�뷴��������
���㣬�뷴��������![]() ��ͼ��ֱ���
��ͼ��ֱ���![]() ��
��![]() ���㣮
���㣮
��1����ͼ����![]() ����
����![]() ���߶�
���߶�![]() �ϣ������
�ϣ������![]() ��
��![]() �غϣ�ʱ������
�غϣ�ʱ������![]() ��
��![]() ���
���![]() ��Ĵ��ߣ�����Ϊ
��Ĵ��ߣ�����Ϊ![]() ��
��![]() ��������
��������![]() �����Ϊ2ʱ�������
�����Ϊ2ʱ�������![]() ��λ�ã�
��λ�ã�
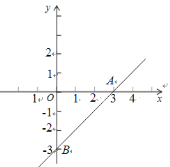
��2����ͼ����![]() ʱ����
ʱ����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ������ڣ������
���ƣ������ڣ������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
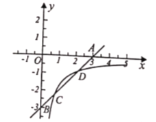
��3����ij�����������ε�һ���߳�Ϊ5���������߳�ǡ������������ͼ��Ľ�������꣬��![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ��
��![]() ����2�����ڣ�
����2�����ڣ�![]() ��
��![]() ����3��
����3��![]()
��������
��1��������֪�����������������ʽ��Ȼ�����ƽ�еõ�![]() ���ó�
���ó�![]() ���ֽ�Ͼ������=
���ֽ�Ͼ������=![]() ������������
������������
��2��������֪�����Ƶ�����E��A����࣬Ȼ�����C,D�������꣬�ٷ���������������ٵ�![]() ���ڵ�
���ڵ�![]() ���ó�
���ó�![]() �������ɵó������
�������ɵó������
��3������һ�κ����ͷ����������Ľ���ʽ�ó������飬��ȥy�ó�����x��һԪ���η��̣����x��ֵ���ٷ��������������������ε����߹�ϵ��⣺��5Ϊ���������ε�������
��5Ϊ���������εױ߳�.�����ó�k��ֵ.
�⣺��1����![]() ʱ��
ʱ��![]() ��
��
��ͼ����![]() �ᣬ
�ᣬ![]() �ᣬ��
�ᣬ��![]() ��
��
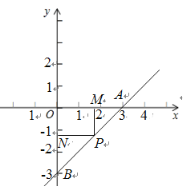
��![]() ����
����![]() �٣�
�٣�
���������Ϊ2����![]() ��.
��.
���ɢ٢ڵ�![]() Ϊ1��2.
Ϊ1��2.
��![]() ��
��![]() .
.
��2����![]() ����
����![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() �㲻������
�㲻������![]() ���Ҳ࣬
���Ҳ࣬
��![]() ��
��![]() �����ʱ��
�����ʱ��![]() ��
��![]()
����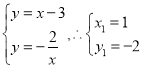 ��
��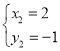
��![]() ��
��![]() .
.
�ٵ�![]() ����
����![]() .
.
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() .
.
��![]() .
.
�ڵ�![]() ����
����![]() ��
��
��![]() ����
����![]() .
.
����������![]() ��
��![]() .
.
��3����![]() ��
��![]() ʱ��
ʱ��
���� ��
��
��![]() ��
��
![]() ��
��
![]() ��
��![]() .
.
�ٵ�5Ϊ���������ε�����ʱ��![]() .
.
�ڵ�5Ϊ���������εױ߳�ʱ��![]() ��
��
��![]() ������ȥ.
������ȥ.
��ˣ����ϣ�![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB��AC����BAC������ֱ��l������A(��������B���C)����C����ֱ��l�ĶԳƵ�Ϊ��D������BD��CD.
(1)��ͼ1��
����֤����B��C��D���Ե�AΪԲ�ģ�ABΪ�뾶��Բ��.
��ֱ��д����BDC�Ķ���(�ú�����ʽ�ӱ�ʾ)Ϊ______.
(2)��ͼ2��������60��ʱ������D��BD�Ĵ�����ֱ��l���ڵ�E����֤��AE��BD.
(3)��ͼ3��������90��ʱ����ֱ��l��CD�Ľ���ΪF������BF.��ֱ��l�Ƶ�A��ת�����߶�BF�ij�ȡ�����ֵʱ��ֱ��д��tan��FBC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����������ʩ��һ����Ͷ�ʹ�˾�ⶨ��ij�����ò軨���¼�����һƬ�˹����������г����飬����![]() ��軨��
��軨��![]() ���¼��ķ�����ͬ������
���¼��ķ�����ͬ������![]() ��軨��
��軨��![]() ���¼�����
���¼�����![]() Ԫ.
Ԫ.
��1����軨���¼������۵��ۣ�
��2���þ���������Ҫ�軨�¼���![]() �꣬Ҫ��軨���¼���
�꣬Ҫ��軨���¼���![]() �꣬���������ֻ����ܷ��ò�����
�꣬���������ֻ����ܷ��ò�����![]() Ԫ��������Ͷ�ʹ�˾�������������ܷ�����ͣ���ͷ����Ƕ���.
Ԫ��������Ͷ�ʹ�˾�������������ܷ�����ͣ���ͷ����Ƕ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����6��6�����纣���գ�ijУ���꼶����������Ϊ����ϧ������Դ�����������������������֪ʶ�������Ϊ�˽�ȫ�꼶500��ѧ���˴ξ����ɼ����ٷ��ƣ�������������ȡ�˲��ֲ���ѧ���ijɼ������������Ƴ����²�������ͳ�Ʊ�����1����ͳ��ͼ����ͼ���������ͼ����Ϣ����������⣺
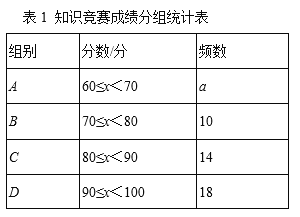

��1�����ε���һ�������ȡ��_____������ѧ���ijɼ���
��2����1��a��_____��
��3������ȡ�IJ���ѧ���ijɼ�����λ�����ڵ����������_____��
��4��������ƣ���У���꼶�����ɼ��ﵽ80�����ϣ���80�֣���ѧ��Լ��_____�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ���ཻ�ڵ�
��ͼ���ཻ�ڵ�![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��
��
��1����![]() ��ֵ��
��ֵ��![]() ��ֵ�Լ���
��ֵ�Լ���![]() �����ꣻ
�����ꣻ
��2���۲췴��������![]() ��ͼ��
��ͼ��![]() ʱ����ֱ��д���Ա���
ʱ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��������
Ϊ��������![]() ��ʹ��
��ʹ��![]() ��
��![]() ���������ϣ���
���������ϣ���![]() �ڵ�һ���ޣ����
�ڵ�һ���ޣ����![]() �����ꣻ
�����ꣻ
��4����y�����Ƿ���ڵ�![]() ��ʹ
��ʹ![]() ��ֵ��С�������ڣ��������
��ֵ��С�������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y��ax2��3ax+c��ͼ����x�ύ�ڵ�A��B����y�ύ�ڵ�cֱ��y����x+4������B��C��
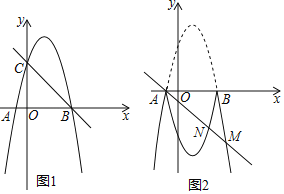
��1���������ߵı���ʽ��
��2������A��ֱ��y��kx+k���������ڵ�M����ֱ��BC�ڵ�N������AC����ֱ��y��kx+kƽ����ABC����������M�����ꣻ
��3����ͼ2����������λ��x���Ϸ���ͼ����x�ᷭ�ۣ���ֱ��y��kx+k�뷭�ۺ������ͼ��ֻ����������ʱ����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC����BAC��90����BC��5��AC��2![]() ����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
��1����BD�ij���
��2������AD�����DAC������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ��ͬʱ������
��ͬʱ������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ����һ����ֹͣ�˶�����һ����Ҳֹͣ�˶������
����һ����ֹͣ�˶�����һ����Ҳֹͣ�˶������![]() ��
��![]() �˶���ʱ����
�˶���ʱ����![]()
![]()
![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��
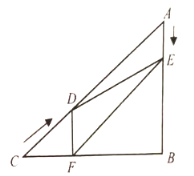
��1��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
��2�����ı���![]() �����Ϊ
�����Ϊ![]() �������
�������![]() ��
��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��3���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() �����ڣ����
�����ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��4����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��һ���ܳ�Ϊ18cm��������ֽƬ��BC=5cm����O����������Բ��С���ü����ڡ�O���Ҳ��������O���е�����һ��ֱ��![]() ������AMN������µ������ε��ܳ�Ϊ�� ��
������AMN������µ������ε��ܳ�Ϊ�� ��
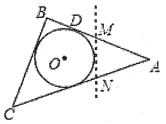
A.![]() B.
B.![]() C.
C.![]() D.��ֱ��
D.��ֱ��![]() �ı仯���仯
�ı仯���仯
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com