
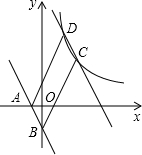
 如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),分析 (1)根据待定系数法即可求得;
(2)分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,设D(m,n),则C(m+1,n-2),根据k1=(m+1)(n-2)=mn,求得m、n的数量关系,设直线AD解析式为y=ax+c(a≠0),将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=5S△ABE,列方程求m、n的值,即可求得C、D的坐标以及k1的值.
解答 解:(1)∵直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
∴$\left\{\begin{array}{l}{-k+b=0}\\{b=-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
故答案是:-2,-2;
(2)如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH与△ABO中,
$\left\{\begin{array}{l}{∠DHC=∠BOA=90°}\\{∠HDC=∠ABO}\\{DC=BA}\end{array}\right.$,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2.
设D(m,n),则C(m+1,n-2),
则(m+1)(n-2)=mn=k1,
解得n=2m+2,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b(a≠0),将A、D两点坐标代入得
$\left\{\begin{array}{l}{-a+b=0①}\\{ma+b=2m+2②}\end{array}\right.$,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则 $\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,
∴y=2x+2,E(0,2),BE=4,
∴S△ABE=$\frac{1}{2}$×BE×AO=2,
∵S四边形BCDE=5S△ABE=5×$\frac{1}{2}$×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得m=2,
∴n=2m+2=6,
∴C(3,4),D(2,6),
∴k1=mn=2×6=12.
则该反比例函数的解析式为:y=$\frac{12}{x}$.
点评 本题考查了待定系数法求一次函数的解析式以及反比例函数的解析式,一次函数和反比例函数的交点问题.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | (4,5) | B. | (4,-5) | C. | (5,4) | D. | (5,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
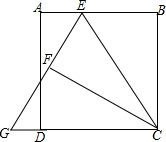 如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).
如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE=$\frac{6t}{9-{t}^{2}}$(用含t的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com