
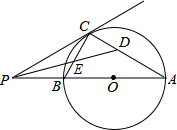
 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.分析 (1)如图,连接OC,根据已知条件得到∠CPD=∠DPA,∠A=∠ACO,根据切线的性质得到OC⊥PC,推出∠DPA+∠A=45°,即∠CDP=45°;根据圆周角定理得到∠ACB=90°,即可得到结论;
(2)根据三角函数的定义得到$\frac{PC}{OC}=\frac{PC}{BC}=\frac{PC}{PB}$$\sqrt{3}$,由PD平分∠APC,得到∠CPD=∠DPA,推出△PCD∽△PEB,根据相似三角形的性质得到$\frac{PD}{PE}=\frac{BE}{CD}=\frac{PC}{PB}$=$\sqrt{3}$,等量代换即可得到结论.
解答 解:(1)如图,连接OC, ∵OC=OA,PD平分∠APC,
∵OC=OA,PD平分∠APC,
∴∠CPD=∠DPA,∠A=∠ACO,
∵PC为⊙O的切线,
∴OC⊥PC,
∵∠CPO+∠COP=90°,
∴(∠CPD+∠DPA)+(∠A+∠ACO)=90°,
∴∠DPA+∠A=45°,
即∠CDP=45°;
∵AB是⊙O的直径,
∴∠ACB=90°,
∴△CED为等腰直角三角形;
(2)∵PC是切线,
∴∠OCP=90°,
∵∠APC=30°,
∴在RT△POC中,cot∠APC=cot30°=$\frac{PC}{OC}=\frac{PC}{BC}=\frac{PC}{PB}$$\sqrt{3}$,
∵PD平分∠APC,
∴∠CPD=∠DPA,
∵∠PEB=∠CED=∠CDE=45°,
∴△PCD∽△PEB,
∴$\frac{PD}{PE}=\frac{BE}{CD}=\frac{PC}{PB}$=$\sqrt{3}$,
∵∠A=∠PCB=∠CPA=30°,
∴AC=PC=$\sqrt{3}$BC,
∴$\frac{BE}{AD}$=$\frac{BE}{AC-CD}$=$\frac{BE}{\sqrt{3}BC-CE}$=$\frac{BE}{\sqrt{3}(BE+\sqrt{3}BE)-\sqrt{3}BE}$=$\frac{1}{3}$.
点评 本题考查了切线的性质,等腰直角三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质,连接OC构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
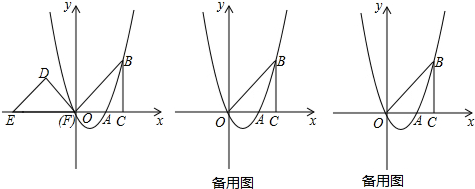
 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
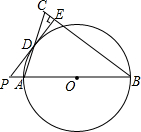 如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.
如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )| A. | $\frac{π+\sqrt{2}-1}{2}$cm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D. | $\frac{π+\sqrt{3}-1}{2}$cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
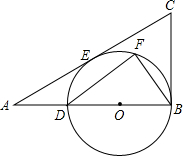 如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.
如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com