
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=6,求菱形的面积.

【答案】(1)证明见解析;(2)24![]()
【解析】试题(1)首先证明△ABC是等边三角形,进而得出∠AEC=90°,四边形AECF是平行四边形,即可得出答案;
(2)利用勾股定理得出AE的长,进而求出菱形的面积.
试题解析:(1)∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,
∴∠AEC=90°,
∵E、F分别是BC、AD的中点,
∴AF=![]() AD,EC=
AD,EC=![]() BC,
BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形,
又∵∠AEC=90°,
∴四边形AECF是矩形;
(2)在Rt△ABE中,AE=![]() ,
,
所以,S菱形ABCD=6×3![]() =18
=18![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生 | A | B | C | D | E | F | |
身高(单位:cm) | 165 | ____ | 166 | ____ | ____ | 172 | |
身高与班级平 | 均身高的差值) | -1 | +2 | ____ | -3 | +4 | ____ |
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的不等式组 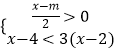 的解集为x>1,且关于x的分式方程
的解集为x>1,且关于x的分式方程 ![]() +
+ ![]() =3有非负整数解,则符合条件的m的所有值的和是( )
=3有非负整数解,则符合条件的m的所有值的和是( )
A.﹣2
B.﹣4
C.﹣7
D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地。假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等,)又顺水航行返回万州,若该轮船从万州出发后所用时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能反映y与x之间函数关系的图象大致是【 】
A. B.
B.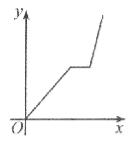 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4.点D是AB边上任意一点,则CD的最小值为 。
(2)如图②,在矩形ABCD中,AB=3,BC=4.点M、N分别在BD、BC上。求CM+MN的最小值.
(3)如图③,在矩形ABCD中,AB=3,BC=4.点E是AB边上的一点,且AE=2,点F是BC边上的任意一点。把△BEF沿EF翻折,点B对应点G,连接AG、CG.四边形AGCD的面积的最小值是 。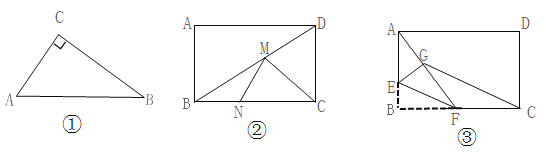
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当![]() 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当![]() 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l:![]() 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线![]() 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com