
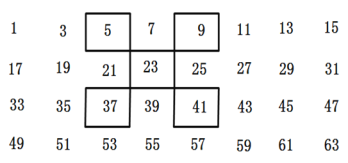
【题目】将连续的奇数1,3,5,7,9,…排成如图所示的数阵.用框框住5个数.
(1)将此框上、下、左、右平移,可以框住另外5个数,若中间的数为a,用代数式表示此框中由小到大的另4个数,并求这五个数的和.
(2)此框中的5个数的和能等于2020吗?若能,请写出这5个数;若不能,请说明理由.
【答案】(1)5a;(2)不能,理由见详解.
【解析】
(1)中间的数为a,左上角的数为(a-18),右上角的数为(a-14),左下角的数为(a+14),右下角的数为(a+18),然后计算它们的和即可;
(2)根据5个数的和为2020,求出a是奇数就可能,不是奇数就不可能.
解:(1)根据题意:设中间的数为a,则左上角的数为:(a-18),右上角的数为:(a-14),左下角的数为:(a+14),右下角的数为:(a+18);
∴这五个数的和为:(a-18 )+( a-14)+( a+14)+(a+18)=5a;
(2)根据题意,得:5a=2020,
解得:a=404;
∵404是偶数,不是奇数,
∴此框中的5个数的和不能等于2020.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】将![]() 沿直线
沿直线![]() 平移到
平移到![]() 的位置,连接
的位置,连接![]() 、
、![]() .
.
(1)如图1,写出线段![]() 与
与![]() 的关系__________;
的关系__________;
(2)如图1,求证:![]() ;
;

(3)如图2,当![]() 是边长为2的等边三角形时,以点
是边长为2的等边三角形时,以点![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系.求出点
轴建立平面直角坐标系.求出点![]() 的坐标,使得以
的坐标,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法,其中正确的有( )
①如果a大于b,那么a的倒数小于b的倒数;②若a与b互为相反数,则![]() =﹣
=﹣![]() ;③几个有理数相乘,负因数的个数是偶数时,积是正数;④如果mx=my,那么x=y,
;③几个有理数相乘,负因数的个数是偶数时,积是正数;④如果mx=my,那么x=y,
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN.
下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE.
其中正确的结论是 .(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
①﹣6﹣(+5)+23+|﹣![]() |
|
②计算:﹣12019+![]() ÷
÷![]() ﹣
﹣![]() ×(﹣9)
×(﹣9)
③计算:[-2﹣8×![]() ]÷(﹣2)3
]÷(﹣2)3
④课堂上老师出了一道计算题。
计算:![]() +
+![]() -(
-(![]() )-14+(
)-14+(![]() ),小明一看,太复杂了,怎么解呢?你能帮助小明解决这个问题吗?试试看。
),小明一看,太复杂了,怎么解呢?你能帮助小明解决这个问题吗?试试看。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上,老师在黑板上出了一道题:在同一平面内,若∠AOB=70°,∠BOC=15°24′36″,求∠AOC的度数.
下面是七年级同学小明在黑板上写的解题过程:
解:根据题意可画出图(如图1)
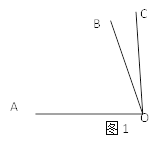
因为∠AOB=70°,∠BOC=15°24′36″,
所以∠AOC=∠AOB+∠BOC
=70°+15°24′36″
=85°24′36″
即得到∠AOC=85°24′36″
同学们在下面议论,都说小明解答不全面,还有另一种情况.请按下列要求完成这道题的求解.
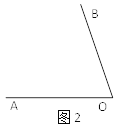
(1)依照图1,用尺规作图的方法将另一种解法的图形在图2中补充完整.
(2)结合第(1)小题的图形写出求∠AOC的度数的完整过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计调查问卷时,下列提问是否合适?如果不合适的话应该怎样改进?
(1)你上学时使用的交通工具是
![]() .汽车
.汽车![]() .摩托车
.摩托车![]() .步行
.步行![]() .其他
.其他
(2)你对老师的教学满意吗?
![]() .比较满意
.比较满意![]() .满意
.满意![]() .非常满意.
.非常满意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )
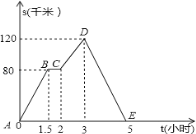
A. 汽车共行驶了120千米
B. 汽车在行驶途中停留了2小时
C. 汽车在整个行驶过程中的平均速度为每小时24千米
D. 汽车自出发后3小时至5小时间行驶的速度为每小时60千米
查看答案和解析>>
科目:初中数学 来源: 题型:
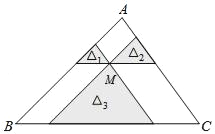
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com