
【题目】将![]() 沿直线
沿直线![]() 平移到
平移到![]() 的位置,连接
的位置,连接![]() 、
、![]() .
.
(1)如图1,写出线段![]() 与
与![]() 的关系__________;
的关系__________;
(2)如图1,求证:![]() ;
;

(3)如图2,当![]() 是边长为2的等边三角形时,以点
是边长为2的等边三角形时,以点![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系.求出点
轴建立平面直角坐标系.求出点![]() 的坐标,使得以
的坐标,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.

【答案】(1)![]() 且
且![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)根据平行四边形的判定与性质即可求解;
(2)过![]() 作
作![]() ,设
,设![]() ,
,![]() ,根据勾股定理与平行四边形的性质即可求解;(3)先根据等边三角形的性质求出
,根据勾股定理与平行四边形的性质即可求解;(3)先根据等边三角形的性质求出![]() ,
,![]() ,
,![]() ,根据平行四边形的性质求出
,根据平行四边形的性质求出![]() ,
,![]() ,再分以
,再分以![]() 为对角线时的一种情况, ②以
为对角线时的一种情况, ②以![]() 为边时的两种情况分别进行讨论求解.
为边时的两种情况分别进行讨论求解.
(1)∵将![]() 沿直线
沿直线![]() 平移到
平移到![]() 的位置,
的位置,
∴AO∥DB,AO=DB,
故答案为:AO∥DB且AO=DB,
(2)解:
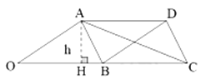
过![]() 作
作![]() ,设
,设![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]()
![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]() 且
且![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]() ,
,![]()
∴![]()
(3)解:如图所示,满足题意的![]() 点坐标有3个。
点坐标有3个。
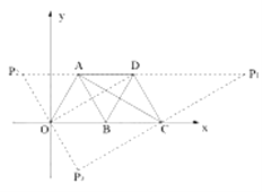
∵等边![]() 的边长为2
的边长为2
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∴![]()
∵![]() ∴
∴![]()
①以![]() 为对角线时,四边形
为对角线时,四边形![]() 为平行四边形
为平行四边形
∴![]() ,
,![]()
∴![]() .
.
②以![]() 为边时,有两种情况:
为边时,有两种情况:
当四边形![]() 为平行四边形时,
为平行四边形时,
![]()
∴![]() .
.
当四边形![]() 为平行四边形时,
为平行四边形时,
![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]() .
.
综上所述,满足题意的![]() 坐标有:
坐标有:![]() ,
,![]() ,
,![]() .
.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月15日是 “国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元,在标价8000元的基础上打9折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售相同的沙发,其成本、标价与甲卖家一致,以前每周可售出5套,现乙卖家先将标价提高m%,再大幅降价40m元,使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了![]() m%,这样一天的利润达到了31250元,求m.
m%,这样一天的利润达到了31250元,求m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
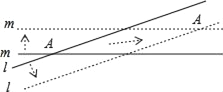
查看答案和解析>>
科目:初中数学 来源: 题型:
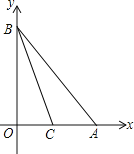
【题目】如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
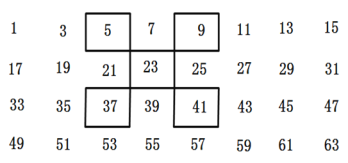
【题目】将连续的奇数1,3,5,7,9,…排成如图所示的数阵.用框框住5个数.
(1)将此框上、下、左、右平移,可以框住另外5个数,若中间的数为a,用代数式表示此框中由小到大的另4个数,并求这五个数的和.
(2)此框中的5个数的和能等于2020吗?若能,请写出这5个数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com